Can you find that number?

We build up the solution digit by digit.

Each of the digits $1-9$ can only be followed by digits that create a multiple of $7$ or $13$ . For instance, a $3$ can only be followed by $5$ or $9$ (making $35$ or $39$ ).

We can summarise these connections as follows:

Note that $70$ is discounted (zero isn't included in the digit list) and so is $77$ (each digit only appears once).

No digit can go before a $7$ . This means the first digit must be a $7$ , and we can immediately see that the first three digits must be $784$ . The next digit must be a $2$ or a $9$ . If it's a $2$ , the next digit can be a $1$ or a $6$ (since $8$ has already been used); if a $9$ , the next digit must be $1$ . Continuing this process, going digit by digit and noting all possible branches (I found seven branches in total, so this is not too onerous), we find there is just one solution, $\boxed{784913526}$ .

Incidentally, we're essentially finding a Hamiltonian path through a directed graph; there are algorithms to do this, but in this case it seemed quicker to just analyse cases.

A stand-alone 7 could be accommodated only at the beginning or end of the number. 70 is eliminated by involving a 0. 77 is eliminated as it involves a doubled digit.

The initial graph. The necessary starting point is obvious; otherwise, one never get a 7 into the number. That confirms the first three digits.

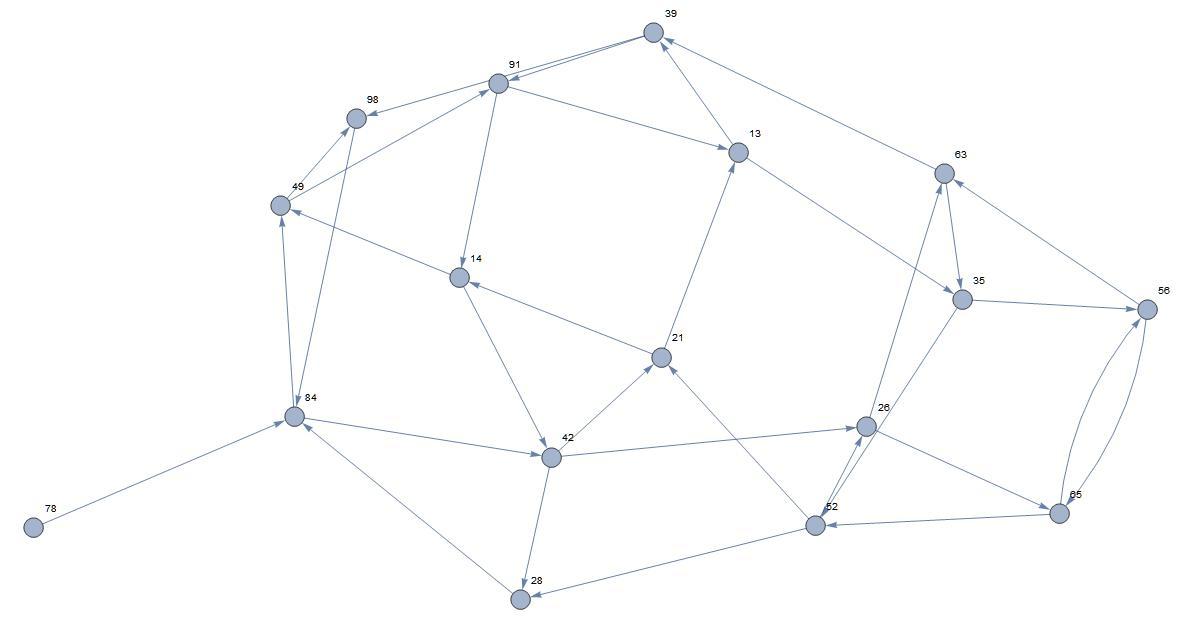
There are only two choices: 42 and 49. 42 leads to a trap. Therefore the next choice must be 49.

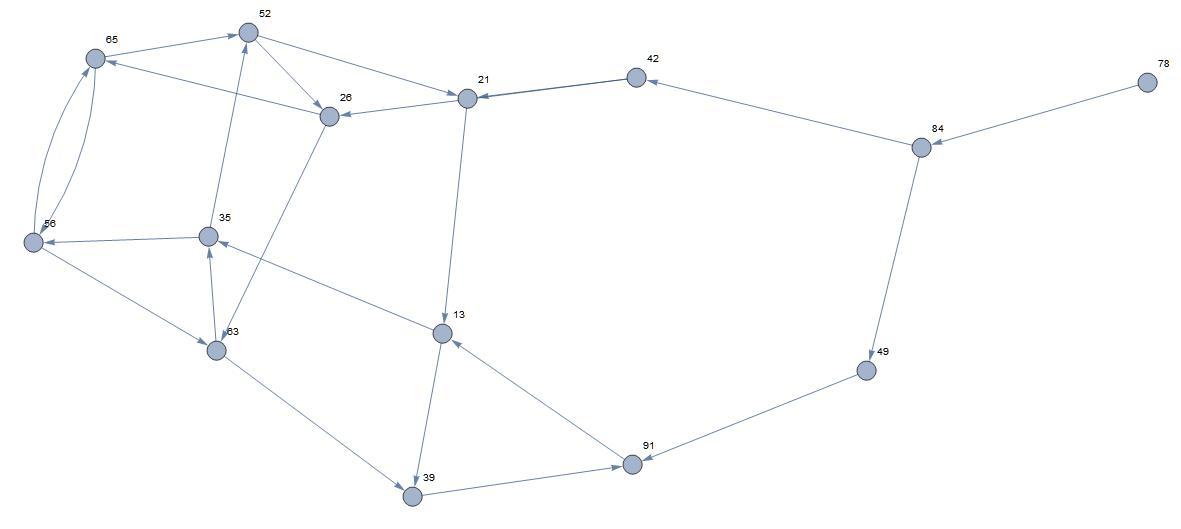
That forces the next three choices: 91, 13 and 35.

The next choice must be 52 for otherwise there is no way to get a digit 2.

And, the solution:

This is not a Hamilton path as not all of the nodes are reached. In fact the graph is trimmed as the digits are reached.

The 2-digit multiples of 7 or 13 are listed below. These are the pieces we have to fit together. Each one has an analysis written next to it. See further down for help navigating the list.

• 07 --> X (0 not included)
• 13 --> Required as (5) for case B.
• 14 --> X (4 already included in 84)
• 21 --> Impossible for case B as 1 already included in 91.
• 26 --> Required as (8) for case B. All requirements met!
• 28 --> X (8 already included in 78)
• 35 --> Required as (6) for case B.
• 39 --> Impossible for case B as 9 already included in 91.
• 42 --> Option for (3) - define case A (failed case).
• 49 --> Option for (3) - define case B.
• 52 --> Required as (7) for case B.
• 56 --> Impossible for case B as no viable number is available to follow it.
• 63 --> Impossible for case B as 3 already included in 13.
• 65 --> Impossible for case B as 5 already included in 35.
• 70 --> X (0 not included)
• 77 --> X (duplicate digit)
• 78 --> (1) Start here; this is the only viable number containing 7!
• 84 --> (2) This is the only number that can follow 78.
• 91 --> required as (4) for case B.
• 98 --> X (8 already included in 78)

Key:

• X - Immediately eliminated
• Regular text - Eliminated at some point in the process
• Bold text - Necessary for the sequence
• ** Bold Italic text** - Immediately identified for the sequence
• ( $n$ ) - Marks the $n$ th 2-digit number in the sequence.

Explanation: We need to find eight 2-digit numbers with consecutive numbers sharing the digit between them. First, we identify 78 and 84 as the first two numbers. We then have a choice between 42 and 49, labeled "case A" and "case B" respectively, and must explore each to determine which is correct. Here you will find the process for case B only ; if you try out case A, you will find that no viable sequences are available. Read the Italic lines in the order they have been labeled to see the reasoning for case B.

This is the IMSO problem but I dont remember exactly year. There are only 78 divisible by 13. And only 84 divisible by 7. So we have 3 first numbers is 784 then ....