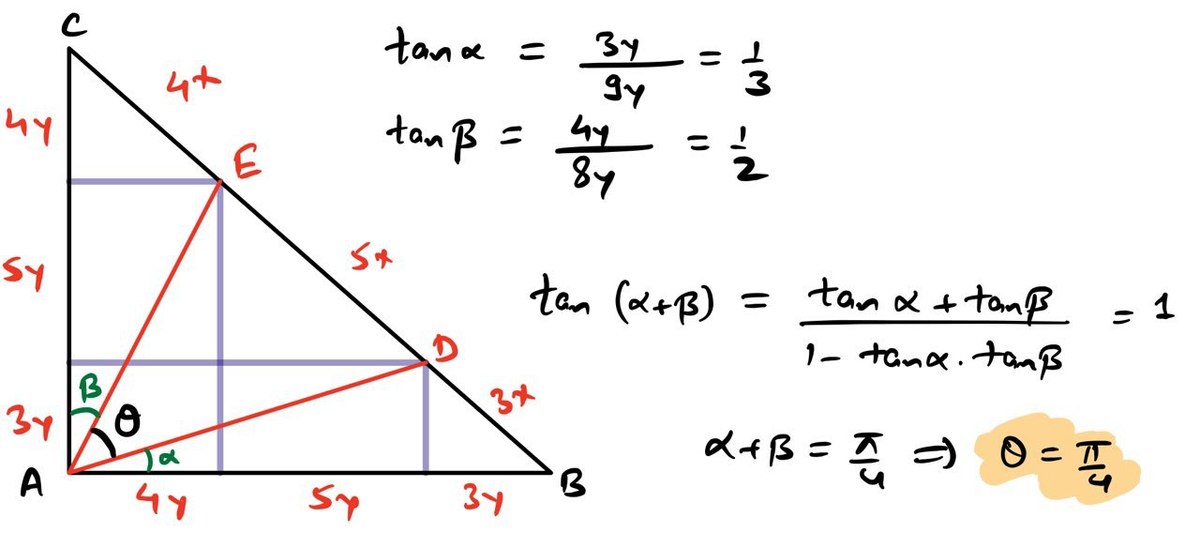Can you solve this RMO question?
Let ABC be a triangle with ∠A = 90◦ and AB = AC. Let D and E be points on the segment BC such that BD : DE : EC = 3 : 5 : 4. Find ∠DAE in degrees ( RMO 2013 )
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions

Moderator note:
Once we have determined the side lengths of triangle A D E , it is easy to find the angle.
Having found that the angle is 4 5 ∘ , one should consider if there is an alternative approach to arrive that result, which sheds more insight into the problem. For example, 3 : 5 : 4 should remind us of the Pythagorean Triplet.
Is it true that if the ratio is in a pythagorean triplet (with DE as the hypotenuse), then the angle D A E must be 4 5 ∘ ?
It is 4 5 o for 3:5:4 only if it is an i s o s c e l e s right angled triangle. 3:5:4 or any of its multiple is OK. I tried with 5:13:12, the angle was not 45.
DM=15x/sqrt10
Sorry in the first line angle ABC= 45 and not angle BAC.
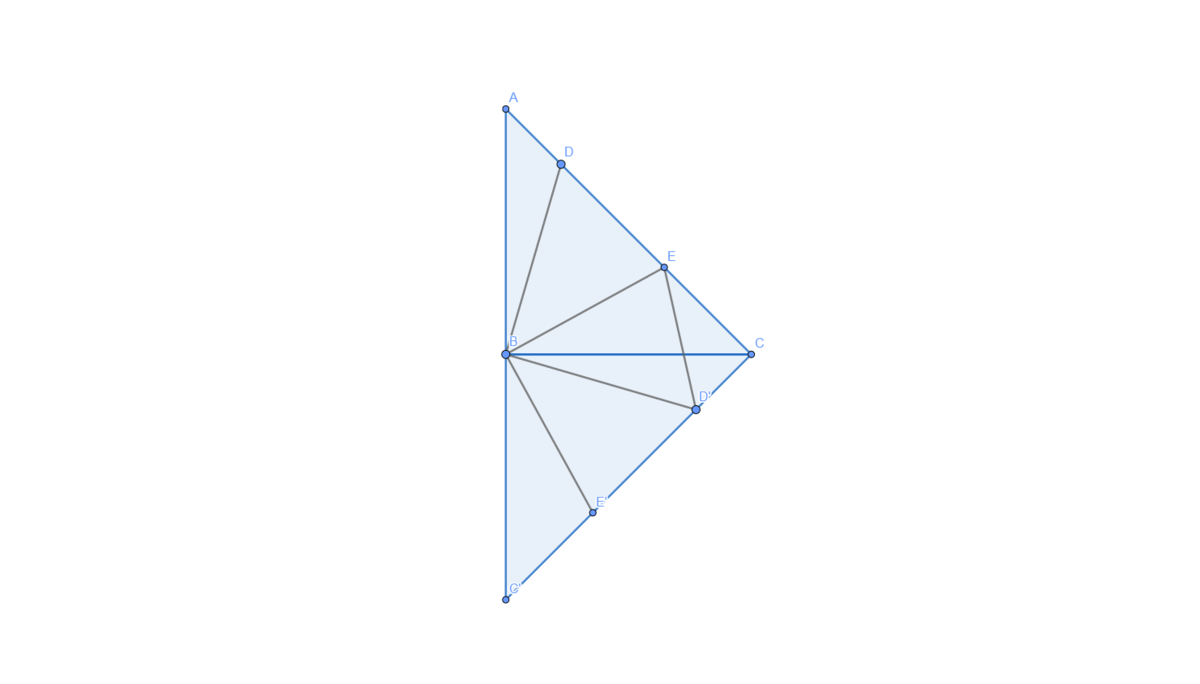
Rotate Δ A B C clockwise by 9 0 ∘ .
Then C D ′ = A D = 3 , C E = 4 , and ∠ E C D ′ = 9 0 ∘ . Therefore E D ′ = 5 = E D .
Thus D E D ′ B is a kite with ∠ D B D ′ = 9 0 ∘ , so ∠ D B E = 4 5 ∘ .
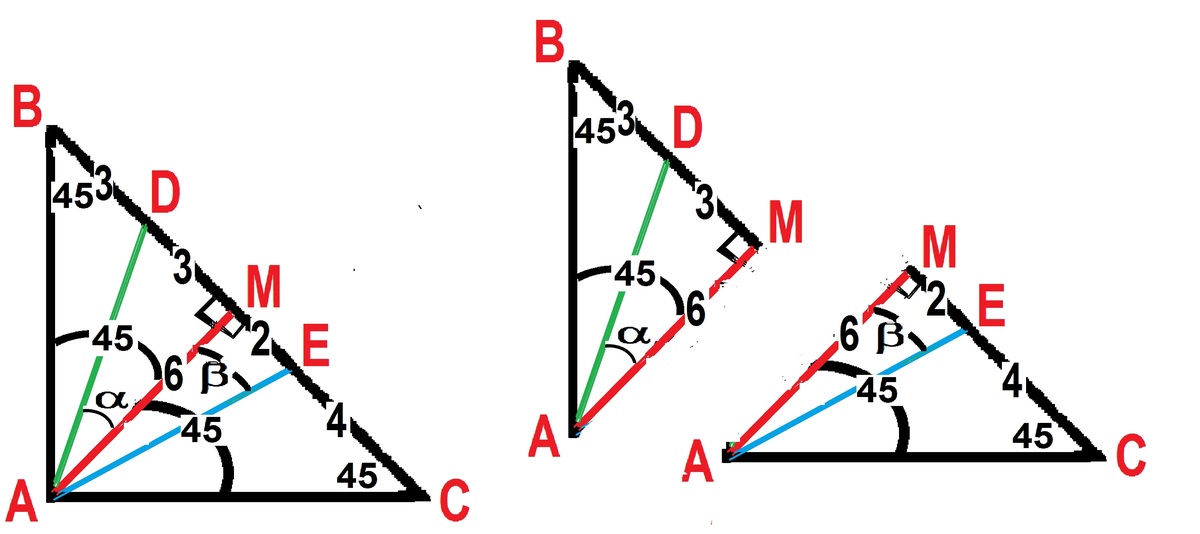
Let M be the midpoint of BC. Without losing generality, let BC=12.
So BD=3, DM=3, ME=2, EC=4 and AM=6.
A
p
p
l
y
i
n
g
S
i
n
L
a
w
t
o
,
Δ
A
D
B
S
i
n
(
4
5
−
α
)
3
=
S
i
n
4
5
A
D
.
.
.
.
(
1
)
Δ
A
D
M
S
i
n
(
α
)
3
=
S
i
n
9
0
A
D
.
.
.
.
(
2
)
Δ
A
E
M
S
i
n
(
β
)
2
=
S
i
n
9
0
A
E
.
.
.
.
(
3
)
Δ
A
E
C
S
i
n
(
4
5
−
β
)
4
=
S
i
n
4
5
A
E
.
.
.
.
(
4
)
F
r
o
m
(
1
)
,
(
2
)
S
i
n
(
4
5
−
α
)
3
=
S
i
n
4
5
S
i
n
(
α
)
3
⟹
S
i
n
α
=
C
o
s
α
−
S
i
n
α
∴
T
a
n
α
=
2
1
.
F
r
o
m
(
3
)
,
(
4
)
S
i
n
(
4
5
−
β
)
4
=
S
i
n
4
5
S
i
n
(
β
)
2
⟹
S
i
n
β
=
C
o
s
β
−
2
S
i
n
β
∴
T
a
n
β
=
3
1
.
∴
∠
D
A
E
=
α
+
β
=
T
a
n
−
1
1
−
2
1
∗
3
1
2
1
+
3
1
=
4
5
o
.
Good problem:easy yet beautiful
Cosine law can also be used though solution will be little lengthy
Much simple than I thought so