Can you find the area?
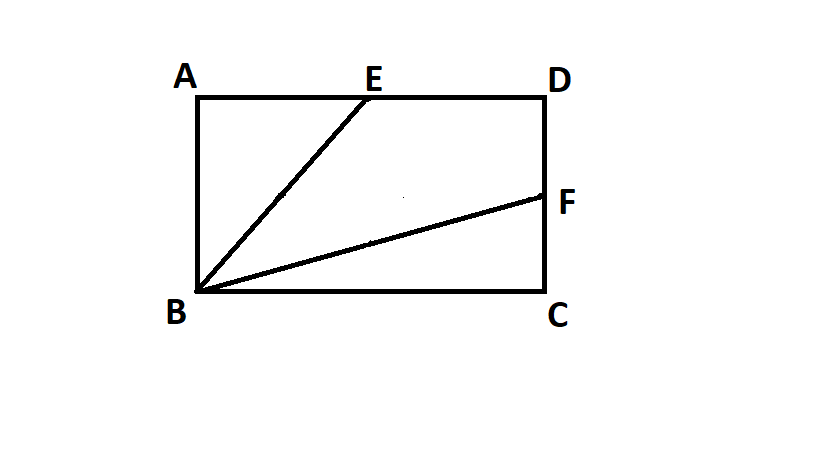 HEY!! suppose that,
ABCD
is a rectangle.
E
,
F
are the midpoints of side
AD
and
CD
respectively.If the AREA of quadrilateral
EBFD
is 9.What is the area of the rectangle
ABCD
?
HEY!! suppose that,
ABCD
is a rectangle.
E
,
F
are the midpoints of side
AD
and
CD
respectively.If the AREA of quadrilateral
EBFD
is 9.What is the area of the rectangle
ABCD
?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Thank you so much for appreciating my effort! HERE is how to crack it: since ABCD is a rectangle,the opposite sides are equal.thus AB=CD and BC=AD . Now,let's consider AB=CD=x and BC=AD=y .so the area of the rectangular is xy .
The area of EBFD=xy- 2 1 . 2 x .y- 2 1 . 2 y .x
or, 9=xy-( 4 x y + 4 x y )
or, 9=xy- 2 x y
or, 9= 2 x y
or, xy=9*2=18.and xy is the area of the rectangle.