Can you find the chord?
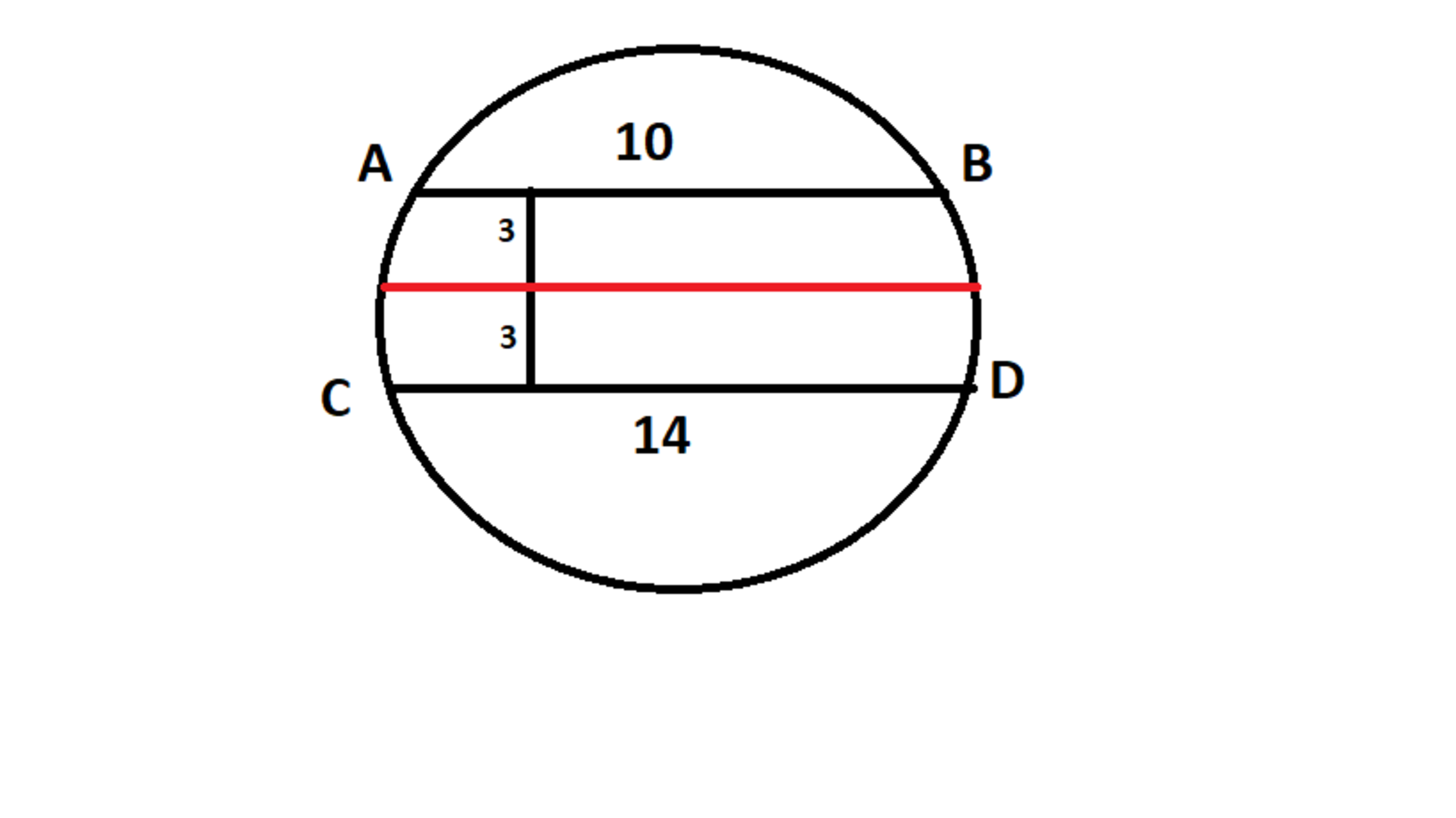In the diagram above, AB and CD are two parallel chords of the circle which have a length of 10 and 14 respectively.The perpendicular distance between them is 6.What would be the length of another chord, which is situated at the same distance from the two chords,(here,its 3).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Okay, We shall be using the rule of two intersecting chords!!
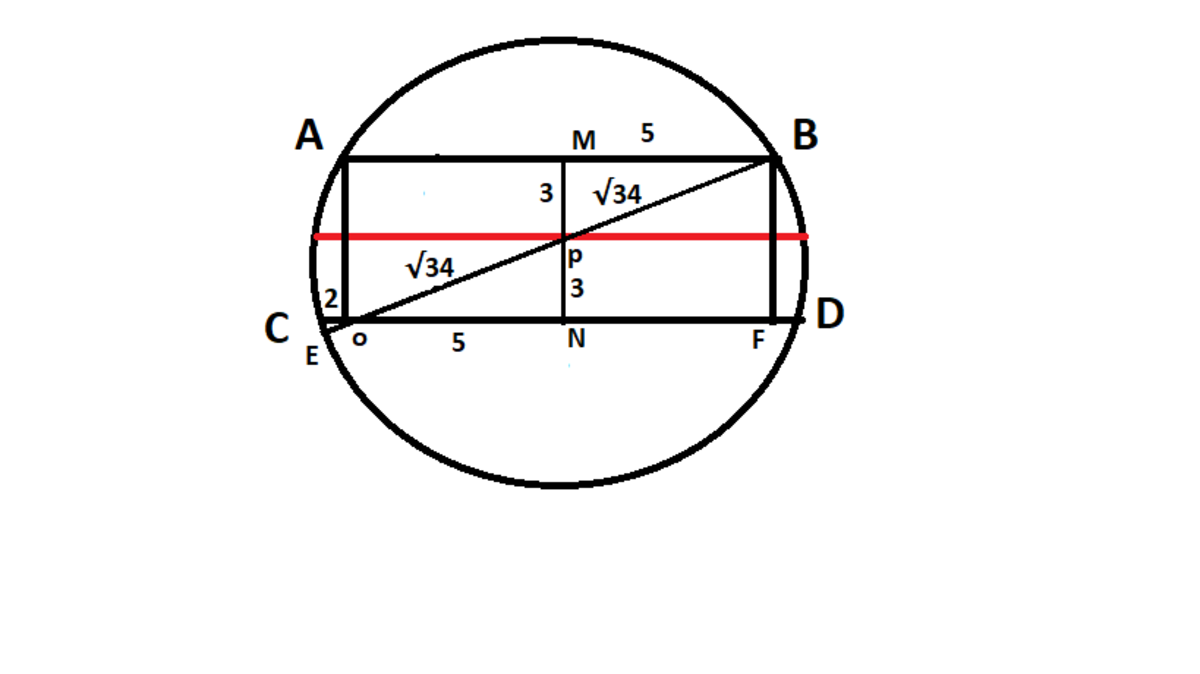In the diagram,
AOFB
is a rectangle with the side lengths of
10
and
6
.We also can say,
CO=FD=2
.
using the rule, OE.BO=CO.DO
or, OE.2√34=2.12
OE= √ 3 4 1 2
The red chord has been bisected at point P .so,lets consider,half of the chord as a .
So, a²=(OE+PO).BP=( √ 3 4 1 2 +√34).√34
Thus, a=√46 and the length of the red chord must be 2a=2.√46