Can you find the length of this line?
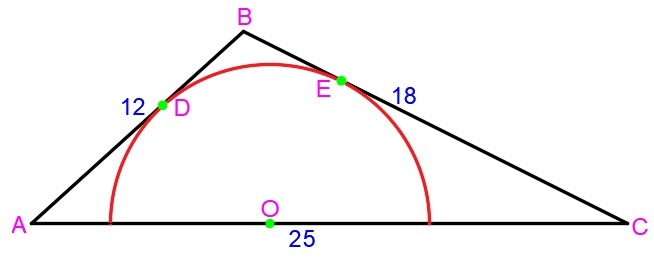 In the triangle shown above,
A
B
=
1
2
,
B
C
=
1
8
and
A
C
=
2
5
,
a semicircle is drawn such that its diameter lies on
A
C
and it is tangent to
A
B
at point
D
and
B
C
at point
E
. Given that point
O
is the center of the semicircle, find the length of
A
O
.
In the triangle shown above,
A
B
=
1
2
,
B
C
=
1
8
and
A
C
=
2
5
,
a semicircle is drawn such that its diameter lies on
A
C
and it is tangent to
A
B
at point
D
and
B
C
at point
E
. Given that point
O
is the center of the semicircle, find the length of
A
O
.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
//Apply Cosine Rule for ∠ A and ∠ C Cosine Rule
cos ( ∠ A ) = 2 × 1 2 × 2 5 1 2 2 + 2 5 2 − 1 8 2 = 1 2 0 8 9
cos ( ∠ C ) = 2 × 1 8 × 2 5 1 8 2 + 2 5 2 − 1 2 2 = 1 8 0 1 6 1
//Apply sin ( θ ) = 1 − cos 2 ( θ )
sin ( ∠ A ) = 1 − cos 2 ( ∠ A ) = 1 2 0 6 4 7 9
sin ( ∠ C ) = 1 − cos 2 ( ∠ C ) = 1 8 0 6 4 7 9
Now let x=AO ⇒ OC=25-x
△ A O D and △ C O E are right angle //since OE and OD are radius
sin ( ∠ A ) = x r a d i u s ⇒ r a d i u s = x ⋅ sin ( ∠ A )
sin ( ∠ C ) = 2 5 − x r a d i u s ⇒ r a d i u s = ( 2 5 − x ) sin ( ∠ C )
⇒ x ⋅ sin ( ∠ A ) = ( 2 5 − x ) sin ( ∠ C )
x = sin ( ∠ C ) + sin ( ∠ A ) 2 5 sin ( ∠ C ) = 1 8 0 6 4 7 9 + 1 2 0 6 4 7 9 2 5 1 8 0 6 4 7 9
multiply denominator and numerator by 6 4 7 9 1 8 0
⇒ x = 2 5 2 5 = 1 0
Right triangles B D O and B E O are congruent, so ∠ D B O = ∠ E B O . Hence, B O bisects ∠ D B E .
Then by angle bisector theorem, C O A O = B C A B = 1 8 1 2 = 3 2 , so A O = 5 2 ⋅ A C = 1 0 .