Can YOU find the length with only one measure?
Geometry
Level
1
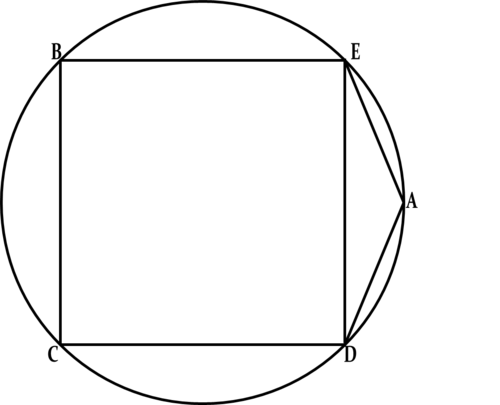 Consider the above diagram, with:
Consider the above diagram, with:
- Square , with a circle circumscribed.
- can be written as , where every variable is equal to a natural number under 10.
- can be written as , where
What is the value of ?
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
B E = 2 2 , since all sides of a square are equal: C D = B E = 2 2 . Easy. Now, to find AE:
The diameter of this circle is also equal to one of square's diagonals. The length of the diagonal of a square is equal to s 2 , where s is a side length. In this case, s = 2 2 , so we get 2 2 ∗ 2 = 2 ∗ 2 = 4 . So, if d is the diameter, d = 4 . The radius, r , is equal to 2 d , which means that r = 2 4 = 1 2 = 2 . Take the center of the circle (and the square as well), and call it Point F. F E = 2 , since that would be half of a diagonal. A F = r = 2 , and Point G is the point of intersection of A F and E D . If we were to find the length of A G , we could create a right triangle with vertices A,G, and E, with A E as the hypotenuse! A G = r − G F . Since it is half of a side (this should be easy to visualize), G F = 2 2 2 = 2 . Therefore, A G = 2 − 2 . Leave that there. Now, E G = G F since they are both halves of sides, so E G = 2 . Now, we can use the Pythagorean Theorem to solve for A E ! 2 2 + ( 2 − 2 ) 2 = A E . If we were to plug this into the variables in the denominator of the problem, we find that it fits perfectly! For B E , 2 2 = 8 , so:
Plugging these variables into the equation for y, we get
y = 2 8 − ( 2 2 ) 2 = 2 5 6 − 4 2 = 2 5 6 − 1 6 = 2 4 0
Plugging our new value into the next equation, we find
8 2 4 0 = 1 3 0
Since the GCF of the numbers in that second fraction is 1, that means that
Plug THESE into the last equation:
x = 3 0 − 1 = 2 9
Therefore, our answer is 2 9 !