Can you find the perimeter?
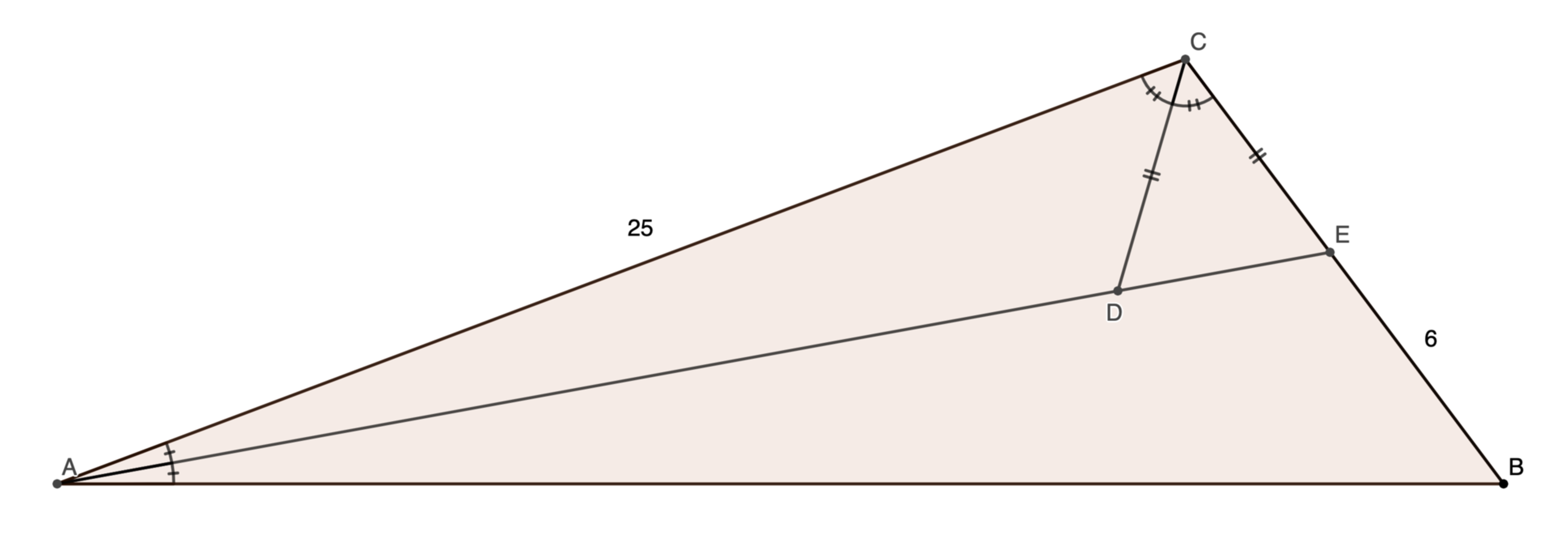
In △ A B C , A C = 2 5 , E B = 6 , ∠ E A C = ∠ B A E , ∠ A C D = ∠ D C E , and C D = C E . What is the perimeter of △ A B C ?
The answer is 66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
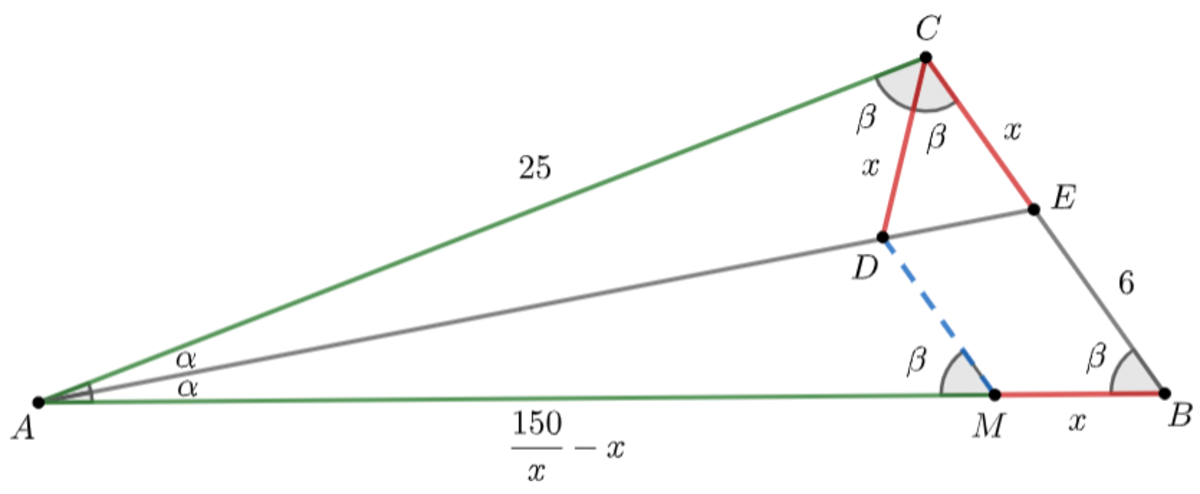 Construction:
Draw line segment
D
M
such that
D
M
∥
B
C
and
M
lies on
A
B
.
Construction:
Draw line segment
D
M
such that
D
M
∥
B
C
and
M
lies on
A
B
.
Let ∠ E A C = ∠ B A E = α and ∠ A C D = ∠ D C E = β , by exterior angle property , ∠ C D E ∠ A B E = ∠ C E D = ∠ D A C + ∠ D C A = α + β = ∠ D M A = ∠ C E D − ∠ E A B = β Let C D = C E = x , since ∠ C B M = ∠ B C D = β and D M ∥ B C , B C D M is an isosceles trapezium ⟹ B M = C D = x .
By Angle Bisector Theorem , A B A C = E B C E ⟹ A B 2 5 = 6 x ⟹ A B = x 1 5 0 Observe, ∠ D M A = ∠ D C A = β , ∠ D A C = ∠ D A B = α ⟹ △ A D M ≅ △ A D C . So, we have, A M x 1 5 0 − x x 2 + 2 5 x − 1 5 0 ( x − 5 ) ( x + 3 0 ) ⟹ x = A C = 2 5 = 0 = 0 = 5 Therefore, perimeter of △ A B C = A B + B C + C A = 3 0 + 1 1 + 2 5 = 6 6
Can't get my head around angle ABE = beta. How did we get there?
Log in to reply
∠ E A B + ∠ A B E = ∠ C E A = α + β . It follows that ∠ A B E = β .
Ah ok, i overlooked that tnx.
Log in to reply
No problem, hope the rest of the solution is clearly written :)
Label the diagram as follows:
By the exterior angle theorem, ∠ C D E = α + β , and since base angles of isosceles triangle are congruent, ∠ C E D = ∠ C D E = α + β , and by the exterior angle theorem, ∠ C B A = β . Therefore, △ C D A ∼ △ B E A by AA similarity, so that x w = 6 w + z .
By the angle bisector theorem, 2 5 x = y 6 , which rearranges to y = x 1 5 0 , and w 2 5 = z x , which rearranges to w = x 2 5 z .
Substituting y = x 1 5 0 and w = x 2 5 z into x w = 6 w + z leads to x 2 + 2 5 x − 1 5 0 = 0 , which has a solution of x = 5 for x > 0 .
If x = 5 , then y = x 1 5 0 = 5 1 5 0 = 3 0 , so that the perimeter is P = 2 5 + x + 6 + y = 2 5 + 5 + 6 + 3 0 = 6 6 .