Can you find the value of f ′ ( 2 0 π ) ?
 Let
f
(
x
)
be a function defined for all
x
∈
R
such that
f
(
x
+
y
)
=
f
(
x
)
⋅
f
(
y
)
for all
x
,
y
∈
R
. Let
f
′
(
0
)
=
1
8
and
f
(
2
0
π
)
=
2
1
. What is the value of
f
′
(
2
0
π
)
?
Let
f
(
x
)
be a function defined for all
x
∈
R
such that
f
(
x
+
y
)
=
f
(
x
)
⋅
f
(
y
)
for all
x
,
y
∈
R
. Let
f
′
(
0
)
=
1
8
and
f
(
2
0
π
)
=
2
1
. What is the value of
f
′
(
2
0
π
)
?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
For completeness, you should demonstrate that there exists at least one function which satisfies the conditions.
Note: I would prefer that you explicitly state that f is differentiable at 0, though that is implicitly assumed in stating that f ′ ( 0 ) = 1 8 .
Log in to reply
That is precisely the issue. The only differentiable functions that satisfy f ( x + y ) = f ( x ) f ( y ) are f ( x ) = 0 and f ( x ) = c x , where c is a positive constant. (In fact, these are the only continuous functions.) And none of them satisfy the given conditions.
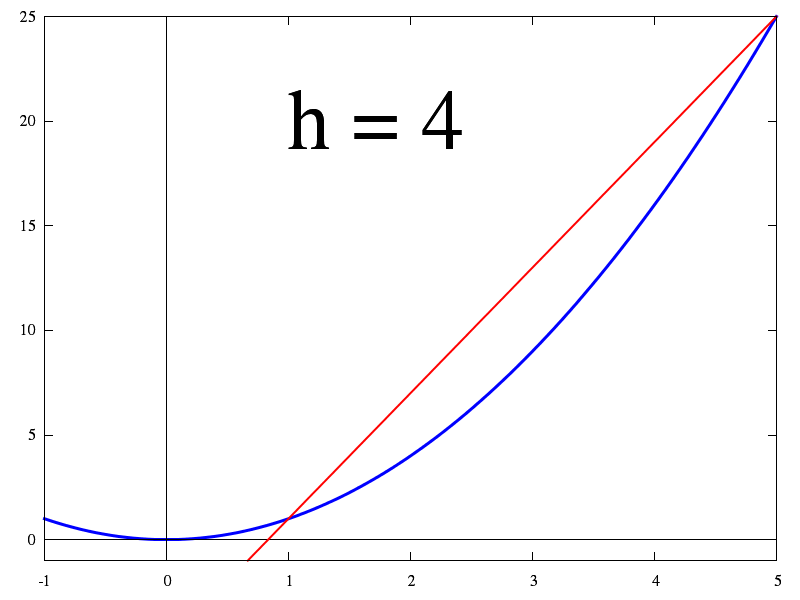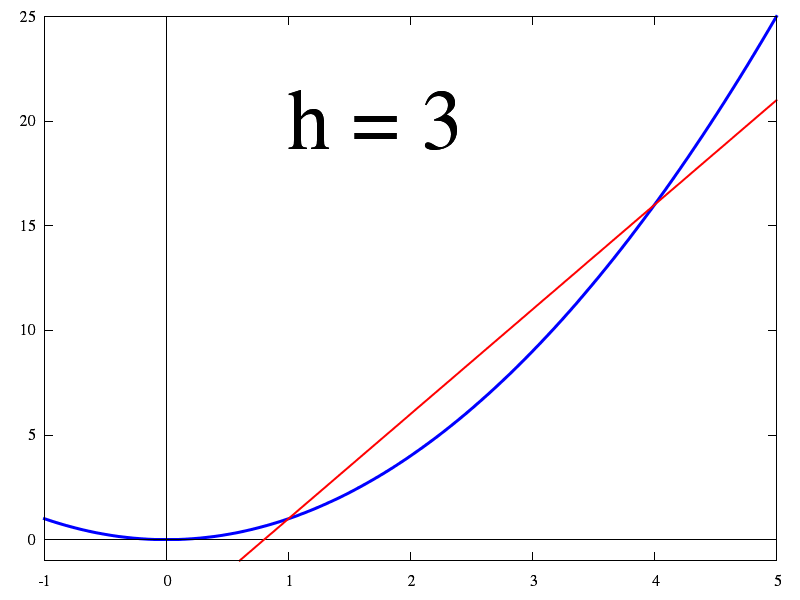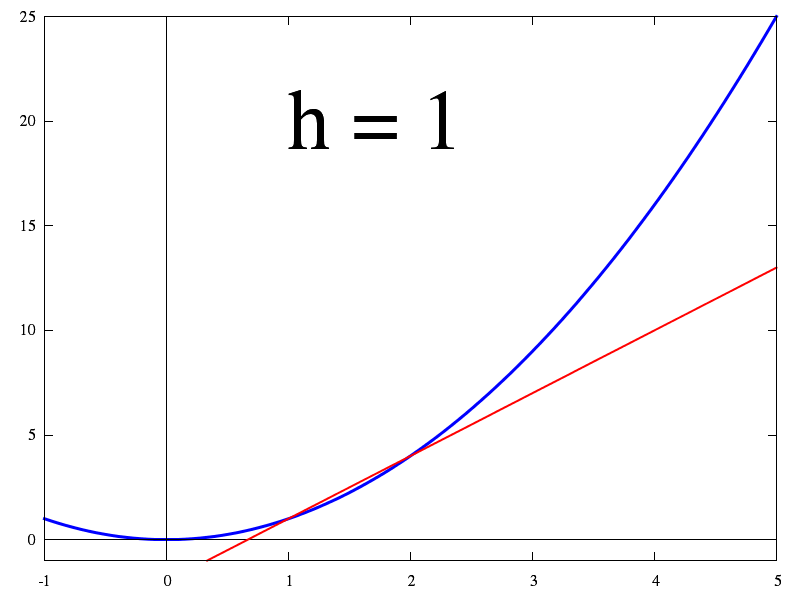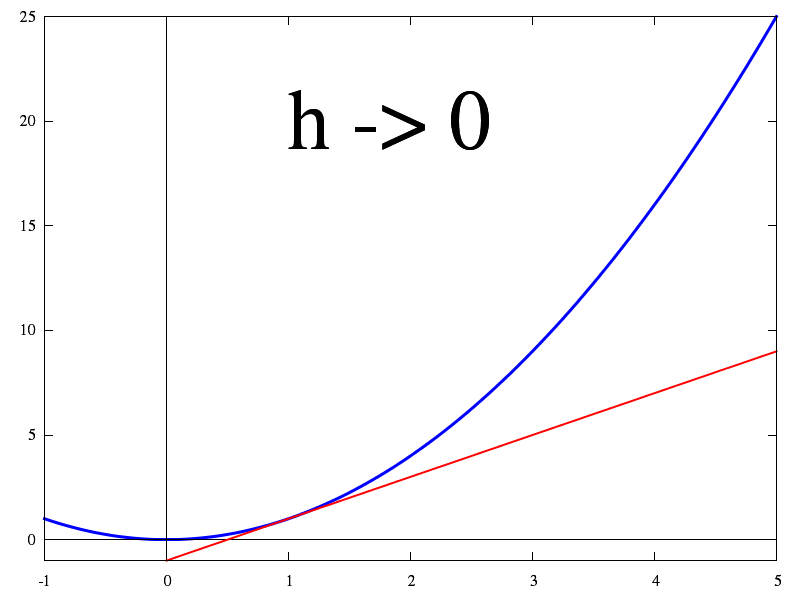
By the definition of the derivation:
\eqalign{ f'(x)&=\lim\limits_{h\to0}\dfrac {f(x+h)-f(x)}{h}=\lim\limits_{h\to0}\dfrac {f(x+h)-f(x+\color{#D61F06}0)}{h} \\ &=\lim\limits_{h\to0}\dfrac {f(x)f(h)-f(x)f(0)}{h} \\ &=\lim\limits_{h\to0}f(x)\dfrac {f(h)-f(0)}{h-0}=f(x)\underbrace{\lim\limits_{h\to0}\dfrac {f(h)-f(0)}{h-0}}_{\text{definition of the derivative at }0} \\ &=f(x)\cdot f'(0)=18\cdot f(x). }
Plugging in x = 2 0 π we get that:
f ′ ( 2 0 π ) = 1 8 ⋅ f ( 2 0 π ) = 1 8 2 1 = 9 .