One of the crown jewels of modern geometry
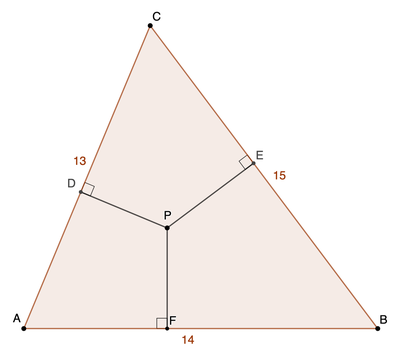
△ A B C is a 13-14-15 triangle. P is chosen so that the sum, P E 2 + P F 2 + P D 2 , is minimized. Express A F as b a where a and b are coprime positive integers, and submit a + b .
The answer is 1968.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
@Fletcher Mattox - Did I miss the jewel?
@Thanos Petropoulos I am so glad you asked! Did you notice that P is the Symmedian point, which Ross Honsberger describes as a crown jewel of modern geometry in his classic "Episodes in Nineteenth and Twentieth Century Euclidean Geometry".
Log in to reply
Thank you very much for pointing out this property of the symmedian point (easy to prove with the identity Lemoin used). I hadn't noticed this nice exercise in the Episodes. Today I learned something new for this jewel.
Let P E = h a , P D = h b , and P F = h c . Then the area of △ A B C is given by A = 2 a h a + b h b + c h c , where a , b , and c are the side lengths opposite angles A , B , and C respectively (not to be confused with answer expression b a ). In this case, 1 3 h b + 1 4 h c + 1 5 h a = 1 6 8 . By Cauchy-Schwarz inequality , we have:
( 1 3 h b + 1 4 h c + 1 5 h a ) 2 ⟹ h a 2 + h b 2 + h c 2 ≤ ( 1 3 2 + 1 4 2 + 1 5 2 ) ( h a 2 + h b 2 + h c 2 ) ≥ 1 3 2 + 1 4 2 + 1 5 2 1 6 8 2
And equality occurs when 1 3 h b = 1 4 h c = 1 5 h a or h a = 5 9 2 5 2 , h b = 2 9 5 1 0 9 2 , and h c = 2 9 5 1 1 7 6 . We also note that:
A F = 1 2 5 ( h c + 1 3 5 h b ) + 1 3 1 2 h b = 2 9 5 1 6 7 3
Therefore the required answer is 1 6 7 3 + 2 9 5 = 1 9 6 8 .
Place the points so that they are at A ( 0 , 0 ) , B ( 1 4 , 0 ) , C ( 5 , 1 2 ) , and P ( p , q ) .
Then A C is on the line 1 2 x − 5 y = 0 and C B is on the line 4 x + 3 y − 5 6 = 0 , and by the distance from a point to a line equation , P D 2 = ( 1 3 1 2 p − 5 q ) 2 , P E 2 = ( 5 4 p + 3 q − 5 6 ) 2 , and P F 2 = q 2 . That means:
P E 2 + P F 2 + P D 2
= ( 5 4 p + 3 q − 5 6 ) 2 + q 2 + ( 1 3 1 2 p − 5 q ) 2
= 4 2 2 5 6 3 0 4 p 2 + 4 2 2 5 1 0 5 6 p q − 2 5 4 4 8 p + 4 2 2 5 6 3 7 1 q 2 − 2 5 3 3 6 q + 2 5 3 1 3 6
= 8 3 2 3 2 5 8 ( 3 9 4 p + 3 3 q − 2 3 6 6 ) 2 + 5 8 1 1 5 1 ( 2 9 5 q − 1 1 7 6 ) 2 + 2 9 5 1 4 1 1 2
which has a minimum of 2 9 5 1 4 1 1 2 when 3 9 4 p + 3 3 q − 2 3 6 6 = 0 and 2 9 5 q − 1 1 7 6 = 0 .
These two equations solve to p = 2 9 5 1 6 7 3 and q = 2 9 5 1 1 7 6 .
Therefore, A F = p = 2 9 5 1 6 7 3 , so a = 1 6 7 3 , b = 2 9 5 , and a + b = 1 9 6 8 .
By Lagrange's Identity , we have ( a 2 + b 2 + c 2 ) ( P E 2 + P F 2 + P D 2 ) = ( a ⋅ P E + b ⋅ P F + c ⋅ P D ) 2 + ( a ⋅ P F − b ⋅ P E ) 2 + ( a ⋅ P D − c ⋅ P E ) 2 + ( b ⋅ P D − c ⋅ P F ) 2 . Since the quantities a 2 + b 2 + c 2 and a ⋅ P E + b ⋅ P F + c ⋅ P D (the latter is twice the area of Δ A B C ) are fixed, to minimize P E 2 + P F 2 + P D 2 , we must have k P E = b P F = c P D = k where k is some constant.
Therefore, we have k = a 2 + b 2 + c 2 2 A Δ A B C = 2 9 5 8 4 . Now, set up a cartesian coordinate system where A ( 0 , 0 ) , B ( 1 4 , 0 ) , C ( 5 , 1 2 ) are the vertices of the triangle. Let ( x , y ) be the coordinate of P , we need to locate the x -coordinate which is the length A F . The line A C is given by the equation A C : 5 y − 1 2 x = 0 so the distance from point P to line A C is 1 3 ∣ 5 y − 1 2 x ∣ = k ⋅ 1 3 = 2 9 5 1 0 9 2 but we know that y = k ⋅ 1 4 = 1 9 5 1 1 7 6 , substituting it back yields x = 2 9 5 1 6 7 3 ( x > 0 ) .
Nice approach!
Let P = ( x , y )
The sum P F 2 + P E 2 + P D 2 = ( P A ⋅ u 1 ) 2 + ( P B ⋅ u 2 ) 2 + ( P C ⋅ u 3 ) 2 = ( P − A ) T u 1 u 1 T ( P − A ) + ( P − B ) T u 2 u 2 T + ( P − C ) T u 3 u 3 T ( P − C )
where u 1 , u 2 , u 3 are unit vectors orthogonal to A B , B C , C A respectively.
Thus u 1 = ( 0 , 1 ) , u 2 = ( 5 4 , 5 3 ) , u 3 = ( 1 3 1 2 , − 1 3 5 )
The expression for the sum of the squared distances can be further simplifed as follows
P F 2 + P E 2 + P D 2 = P T Q P + b T P + c = f ( P )
where Q = u 1 u 1 T + u 2 u 2 T + u 3 u 3 T , b = − 2 ( u 1 u 1 T A + u 2 u 2 T B + u 3 u 3 T C ) , c = A T u 1 u 1 T A + B T u 2 u 2 T B + C T u 3 u 3 T C
Since u 1 u 1 T , u 2 u 2 T , u 3 u 3 T are positive semi-definite, and the vectors u 1 , u 2 , u 3 are not collinear, then Q is positive definite, then our objective function f ( P ) attains its minimum at P ∗ = − 2 1 Q − 1 b . This is easy to show by completing the square.
The rest is numerical computations, which are as follows:
First, we have A = ( 0 , 0 ) , B = ( 1 4 , 0 ) , C = ( 5 , 1 2 )
Secondly,
u 1 u 1 T = [ 0 0 0 1 ]
u 2 u 2 T = 2 5 1 [ 1 6 1 2 1 2 9 ]
u 3 u 3 T = 1 6 9 1 [ 1 4 4 − 6 0 − 6 0 2 5 ]
Therefore,
Q = 4 2 2 5 1 [ 6 3 0 4 5 2 8 5 2 8 6 3 7 1 ]
b = ( − 2 ) ( 2 5 2 2 4 , 2 5 1 6 8 )
Hence,
Q − 1 = 9 4 4 0 1 [ 6 3 7 1 − 5 2 8 − 5 2 8 6 3 0 4 ]
And,
P ∗ = − 2 1 Q − 1 b = ( 2 9 5 1 6 7 3 , 2 9 5 1 1 7 6 )
Hence the required distance A F = 2 9 5 1 6 7 3 , and therefore the answer is 1 6 7 3 + 2 9 5 = 1 9 6 8 .
Looking at the picture, it is clear that fixing the distances AD and BE will uniquely determine the location of point P, which is at the intersection.
Define A D = r , B E = s , D P = t , E P = u , F P = y , A F = x The outline of this solution is
- establish the angles
- to express t, u and y in terms of r and s
- find r and s by setting d ( u 2 + t 2 + y 2 ) / d r and d ( u 2 + t 2 + y 2 ) / d s to 0
- find AF
Establish the angles
Let the interior angles at A , B , C be α , β , γ respectively
Apply the cosine rule: cos α = 2 ⋅ 1 3 ⋅ 1 4 1 3 2 + 1 4 2 − 1 5 2 = 3 6 4 1 4 0 = 1 3 5 ; sin α = 1 − cos 2 α = 1 3 1 2 This way we get
| cos α = 1 3 5 | sin α = 1 3 1 2 | α ≈ 6 7 . 3 8 ° |
| cos β = 5 3 | sin β = 5 4 | β ≈ 5 1 . 1 3 ° |
| cos γ = 6 5 3 3 | sin γ = 6 5 5 6 | γ ≈ 5 9 . 4 9 ° |
Express t, u and y in terms of r and s
Setting the origin in A, use the sine and cosine values to express coordinates in terms of r,s,t and u: D = ( 1 3 5 r , 1 3 1 2 r ) E = ( 1 4 − 5 3 s , 5 4 s ) P = ( x , y ) = ( 1 3 5 r + 1 2 t , 1 3 1 2 r − 5 t ) = ( 1 4 − 5 3 s + 4 u , 5 4 s − 3 u )
Using the two expressions for x and the two expressions for y, we can eliminate u and t. 6 5 x = 2 5 r + 6 0 t = 9 1 0 − 3 9 s − 5 2 u 6 5 y = 6 0 r − 2 5 t = 5 2 s − 3 9 u Combine these to express t and u in terms of r and s: t = 5 6 5 4 6 + 3 3 r − 6 5 s , u = 5 6 3 5 0 − 6 5 r + 3 3 s and y = 5 4 s − 3 u = 5 6 − 2 1 0 + 3 9 r + 2 5 s
Find r and s
P is such that it minimizes Q ( r , s ) = t 2 + u 2 + y 2 = ( ( 5 4 6 + 3 3 r − 6 5 s ) 2 + ( 3 5 0 − 6 5 r + 3 3 s ) 2 + ( − 2 1 0 + 3 9 r + 2 5 s ) 2 ) / 5 6 2 5 6 2 Q = 4 6 4 7 1 6 + 6 8 3 5 r 2 + 5 9 3 9 s 2 + − 2 5 8 4 4 r − 5 8 3 8 0 s − 6 6 3 0 r s
d Q / d r = 0 ⇒ 6 8 3 5 r − 1 2 9 2 2 − 3 3 1 5 s = 0 d Q / d s = 0 ⇒ 5 9 3 9 s − 2 9 1 9 0 − 3 3 1 5 r = 0 these solve to r = 1 7 2 9 / 2 9 5 , s = 4 8 3 / 5 9
Find AF
t = 5 6 5 4 6 + 3 3 × 1 7 2 9 / 2 9 5 − 6 5 × 4 8 3 / 5 9 = 2 9 5 1 0 9 2 u = 5 6 3 5 0 − 6 5 × 1 7 2 9 / 2 9 5 + 3 3 × 4 8 3 / 5 9 = 5 9 2 5 2 y = 5 6 − 2 1 0 + 3 9 × 1 7 2 9 / 2 9 5 + 2 5 × 4 8 3 / 5 9 = 2 9 5 1 1 7 6 x = 1 3 5 × 1 7 2 9 / 2 9 5 + 1 2 × 1 0 9 2 / 2 9 5 = 2 9 5 1 6 7 3 Since A F = x we should submit 1 6 7 3 + 2 9 5 = 1 9 6 8
The minimum value for t 2 + u 2 + y 2 = 2 9 5 1 4 1 1 2
A B : y = 0 , A C : 1 2 x − 5 y + 6 0 = 0 , B C : 4 x + 3 y − 3 6 = 0 If point P has coordinates ( x , y ) , using the distance between a point and a line formula ,
P D 2 + P E 2 + P F 2 = 1 3 2 ( 1 2 x − 5 y + 6 0 ) 2 + 5 2 ( 4 x + 3 y − 3 6 ) 2 + y 2 : = f ( x , y ) Taking partial derivatives,
f x ( x , y ) = 4 2 2 5 3 2 ( 3 9 4 x + 3 3 ( y − 1 2 ) ) f y ( x , y ) = 4 2 2 5 2 ( − 2 5 7 5 2 + 5 2 8 x + 6 3 7 1 y ) we find the critical numbers:
f x ( x , y ) = 0 f y ( x , y ) = 0 } ⇔ ( x , y ) = ( 2 9 5 1 9 8 , 2 9 5 1 1 7 6 ) Performing the second partials test we see that we have a minimum, hence these are the coordinates of point P . Consequently, we get F ( 2 9 5 1 9 8 , 0 ) and A F = 5 + 2 9 5 1 9 8 = 2 9 5 1 6 7 3 For the answer, a = 1 6 7 3 , b = 2 9 5 , thus a + b = 1 9 6 8 .