Can you find your lost dog

Geometry Level 3

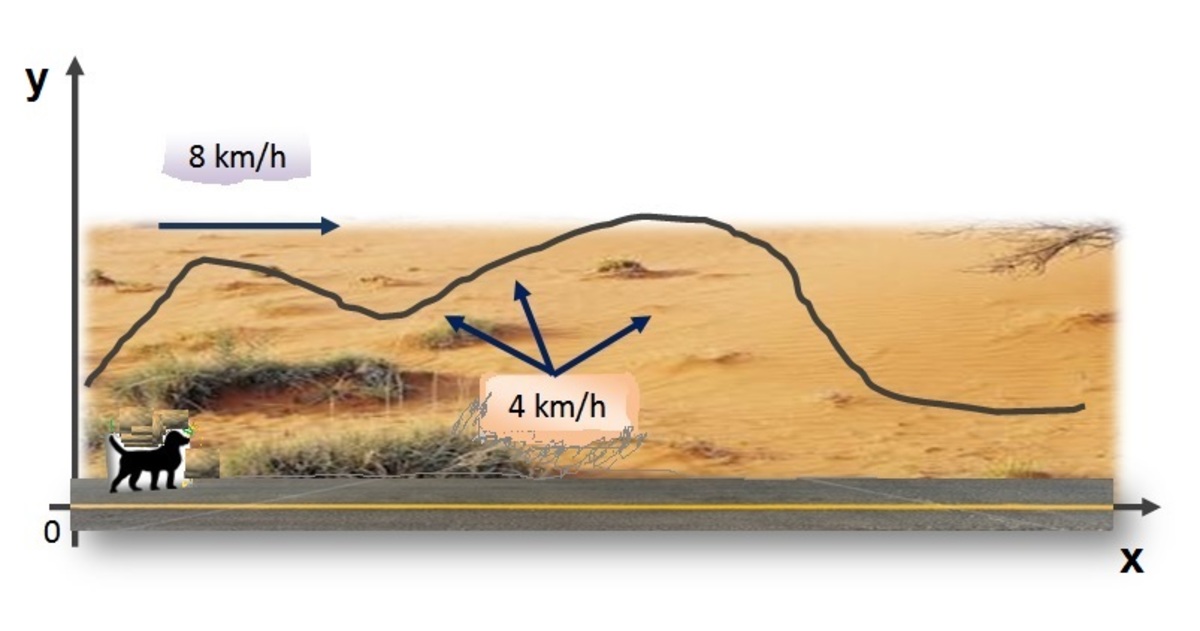
The walk is one of the most important activities you can share with your dog. Assume that you are walking your dog on a straight road as shown in the above figure. At point 0, you left your dog unattended for one hour, the dog can walk along the road at speed of 8 k m / h 8 \ km/h or go through the side field at speed of 4 k m / h 4 \ km/h . How far your dog run is just a function of how far its legs will carry it. Can you determine the domain in which you may find your dog after one hour? Report your answer to this problem as the area of this domain in k m 2 km^2 to the nearest 3 3 decimal places.

Hint : Assume that the domain's boundaries are x-axis, y-axis, and the maximum distances can your dog reach inside the field.


The answer is 18.045.

Ossama Ismail by Ossama Ismail , 63, Egypt

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ossama Ismail
Mar 18, 2017

Maximum reach along the x-axis is: 8 and the maximum reach along the y-axis is 4.

It is easy to show that, the fastest way to reach each any point inside the field is to walk along the road and then to walk along a straight line through the field. If the dog walks a for time = t hour along the x-axis, then it can walk after that in any direction inside the field for time = (1-t) hour (or within a circle with radius = 4 × ( 1 − t ) = 4 \times (1-t) with a center at 8 × t 8 \times t . then the domain is bounded by the red line \color{#D61F06}{\text{red line}} (shown in the figure) that passes through the point (8,0) and is tangent to one of the circles which have centers at ( 8 t , 0 ) (8t,0) and radius = 3 ( 1 − t ) = 3(1-t) . 0.25 ≤ t ≤ 1 0.25 \leq t \leq 1 .

The line equation is y = − x 3 + 8 3 , 2 ≤ x ≤ 8 y = - \dfrac{x}{\sqrt 3} + \dfrac{8}{\sqrt 3 } , \ \ \ 2 \leq x \leq 8

But this line cuts the y-axis at 8 3 > 4 \dfrac{8}{\sqrt 3 } \ > 4 . This contadict that maximum reach in y-axis does not exceed 4.

Then the circle x 2 + y 2 = 4 2 x^2 + y^2 = 4^2 is the circular bound for the domain for 0 ≤ x ≤ 2 0 \leq x \leq 2 .

Then the region in the questions are bounded by:

1. x = 0 , 2. y = 0 , 3. y = − x 3 + 8 3 , 2 ≤ x ≤ 8 4. y = 16 − x 2 , 0 ≤ x ≤ 2 \begin{aligned} 1. \ x &=0, & \\ 2. \ y &=0, & \\ 3. \ y &= - \dfrac{x}{\sqrt 3} + \dfrac{8}{\sqrt 3 } , & 2 \leq x \leq 8 \\ 4. \ y &= \sqrt{16 - x^2}, & 0 \leq x \leq 2 \\ \end{aligned}

Domain area is shown in yellow = △ a r e a + c i r c u l a r s e c t o r a r e a o f 3 0 ∘ = 1 2 × 4 × 8 × sin ⁡ ( 60 ) + 1 12 × π × 4 2 = 18.045 k m 2 \begin{aligned} \\ \text{Domain area is shown in yellow} &= \triangle \ \ area + circular \ sector\ \ area \ of \ \ 30^\circ \\ &= \dfrac{1}{2} \times 4 \times 8 \times \sin(60) +\dfrac{1}{12} \times \pi \times 4^2 = 18.045 \ km^2 \end{aligned}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

I like the problem, but I think I would have liked it even better if the constraint of the coordinate axes had been removed. The result would be merely 4 times larger, so the problem would be essentially the same, but it would feel more natural.

Marta Reece - 4 years, 2 months ago

Log in to reply

I agree with what you said, But, I tried to make it looks simple. I myself like this problem... It took more than 4 hours to write the problem and the answer.

Ossama Ismail - 4 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...