Can you get equality ?

The least number of steps required is seven . I'll use $A,B,C$ to refer to the numbers of balls in the respective boxes. We want to get to $A=B=C=9$ .

Since we need to reduce $C$ from $27$ to $9$ , we need to move at least $18$ balls. After five steps, we've only moved $T_5=1+2+3+4+5=15$ balls; so we need at least six steps.

Next we use a parity argument. Since every step involves box $C$ , odd steps change the parity of $C$ ; even steps don't. After the first step, $C$ will be even; $C$ 's parity follows the pattern even, even, odd, odd, even, even, odd, odd, etc.

These two lines of reasoning show that at least seven steps are required. There are in fact six ways to get to equality in seven steps:

$\begin{aligned} (0,0,27) \to (1,0,26) \to (3,0,24) \to (3,3,21) \to (7,3,17) \to (2,3,22) \to (2,9,16) \to (9,9,9) \\ (0,0,27) \to (1,0,26) \to (3,0,24) \to (3,3,21) \to (3,7,17) \to (3,2,22) \to (9,2,16) \to (9,9,9) \\ (0,0,27) \to (1,0,26) \to (1,2,24) \to (4,2,21) \to (8,2,17) \to (3,2,22) \to (9,2,16) \to (9,9,9) \\ (0,0,27) \to (0,1,26) \to (2,1,24) \to (2,4,21) \to (2,8,17) \to (2,3,22) \to (2,9,16) \to (9,9,9) \\ (0,0,27) \to (0,1,26) \to (0,3,24) \to (3,3,21) \to (7,3,17) \to (2,3,22) \to (2,9,16) \to (9,9,9) \\ (0,0,27) \to (0,1,26) \to (0,3,24) \to (3,3,21) \to (3,7,17) \to (3,2,22) \to (9,2,16) \to (9,9,9) \end{aligned}$

If we achieve equality in $N$ steps, obviously $N \le 9$ , and a total of $\tfrac12N(N+1)$ balls will have been moved. Suppose that $a$ of these have been moved out of box $C$ , and $b$ of these have been moved back into $C$ . Then we must have $a+b \; = \; \tfrac12N(N+1) \hspace{2cm} a - b \; = \; 18$ which implies that $4$ must divide $N(N+1)$ and that $a = \tfrac14N(N+1) + 9$ and $b = \tfrac14N(N+1) - 9$ . Thus we deduce that $N \equiv 0,3 \pmod{4}$ and that $N(N+1) \ge 36$ . The only possible values of $N$ to consider are $N = 7,8$ . The solution for $N=\boxed{7}$ has been found by others, so I won't repeat it.

Here is the Solution

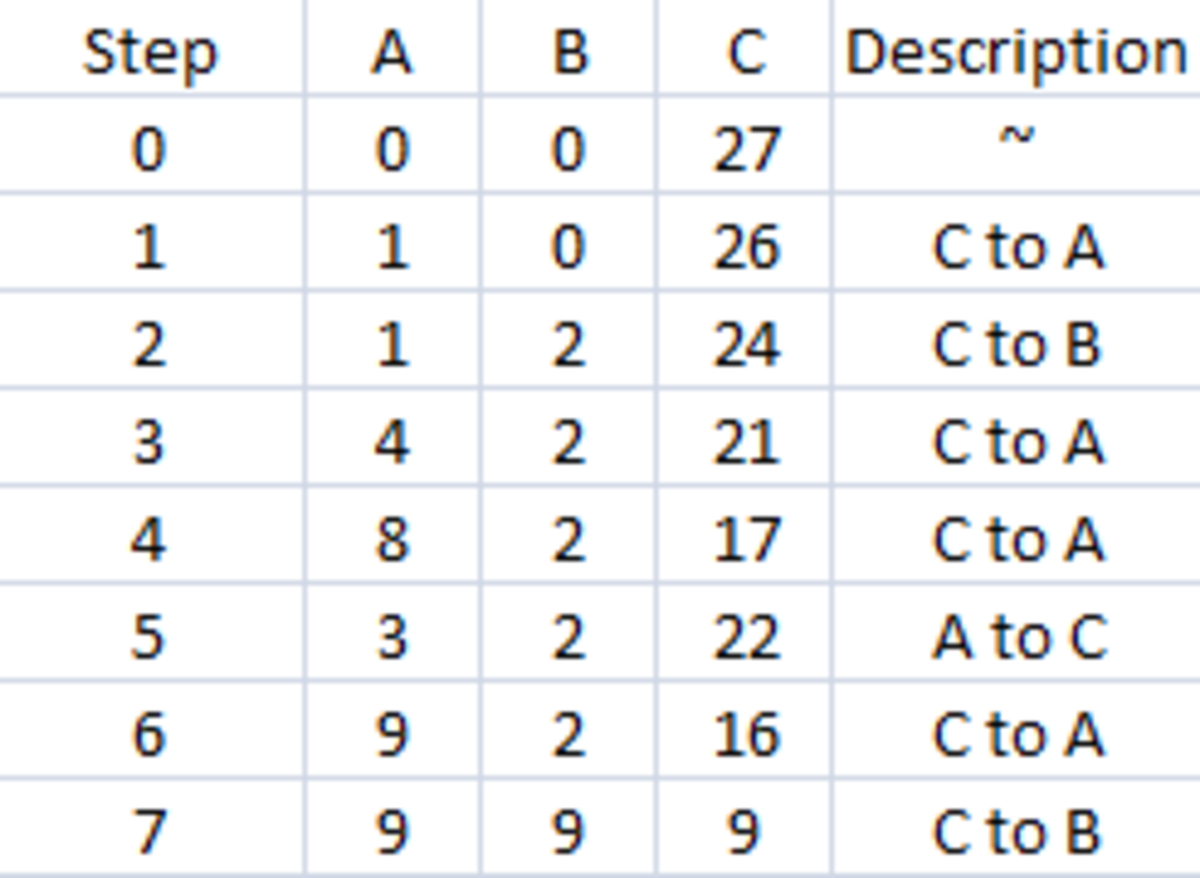
Hence the Answer is :7

Moves (A,B,C) are Starting,(0,0,27)-> (1,0,26)->(3,0,24)->(3,3,21)-> (7,3,17)->(2,3,22)->(2,9,16)-> (9,9,9) Answer=7

N steps to balance 27 balls in $(A, B, C) = (9,9,9)$

• We have to move out 18 balls out of C
• We have to move the exceeding balls back to C.
• The number of exceeding balls should be even number 2N such that we can move back N balls to balance it.

After N steps, we have moved (max.) T balls out of C: $1+2+3+...+N = \cfrac{N(N+1)}{2}$

One of the possible solutions:

$A = (1+3+4 \textcolor{#3D99F6}{-5} +6) \\ B = (2 + 7)$

positive - means move balls from C, negative means move balls from A/B to C.