Can you guess this triangle?

Let the side lengths be $a, a + 1$ and $a + 2$ and the smallest angle be $x$ . The largest angle will be opposite the longest side, and the smallest angle opposite the shortest. So by the Sine rule we have that

$\dfrac{\sin(x)}{a} = \dfrac{\sin(2x)}{a + 2} = \dfrac{2\sin(x)\cos(x)}{a + 2} \Longrightarrow \cos(x) = \dfrac{a + 2}{2a}.$

Now by the Cosine rule we have that

$a^{2} = (a + 1)^{2} + (a + 2)^{2} - 2(a + 1)(a + 2)\cos(x)$

$\Longrightarrow a^{2} = 2a^{2} + 6a + 5 - 2(a + 1)(a + 2)\cos(x)$

$\Longrightarrow \cos(x) = \dfrac{a^{2} + 6a + 5}{2(a + 1)(a + 2)} = \dfrac{a + 5}{2(a + 2)}.$

Thus $\dfrac{a + 2}{2a} = \dfrac{a + 5}{2(a + 2)} \Longrightarrow (a + 2)^{2} = a^{2} + 5a \Longrightarrow a^{2} + 4a + 4 = a^{2} + 5a \Longrightarrow a = 4.$

Thus the side lengths are $4,5,6$ , and the sum of their squares is $16 + 25 + 36 = \boxed{77}.$

I didn't guess it. I worked it out.

Let the natural number side lengths of the triangle be $n$ , $n+1$ and $n+2$ , $\alpha$ be the angle opposite the shortest side $n$ and $\beta$ , opposite $n+1$ , then the remaining angle $\gamma = \pi - \alpha - \beta$ .

Then, using Cosine Rule, we have:

$\cos {\alpha} = \dfrac {(n+1)^2+(n+2)^2-n^2}{2(n+1)(n+2)}\quad \cos {\beta} = \dfrac {n^2+(n+2)^2-(n+1)^2}{2n(n+2)}$

Finding out $\alpha$ and $\beta$ for $n=1,2,3...$ , we have the following table.

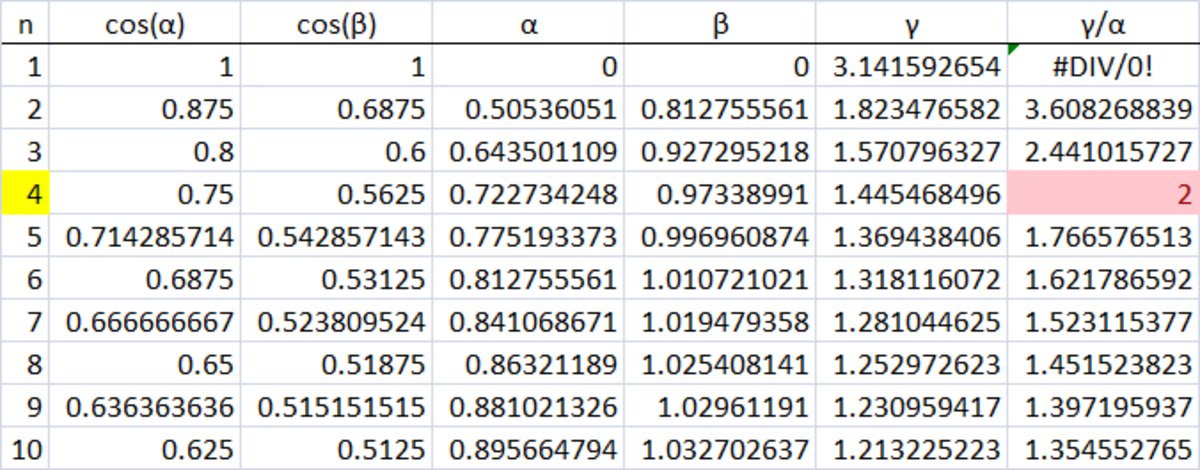
We note that for triangle with side lengths $4$ , $5$ and $6$ , $\gamma = 2\alpha$ . It is therefore, the triangle we need.

Therefore, the required answer is $4^2+5^2+6^2 = \boxed{77}$

$With\ usual\ notation\ for\ \triangle\ ABC, \ \ \ \ \ \ \ \angle\ A=\angle 2C,\ \ \ \therefore\ SinA=Sin2C=2SinC*CosC.\\ Also\ B=180 - 3C.\ \ \ \ \ Sin(180 - 3C)=Sin3C=3SinC - 4Sin^3C=SinC*(4Cos^2C - 1).\\ a=b+1,\ \ c=b-1.\ \ \ \ \ \ Using\ Sin\ Law,\\ \dfrac{a}{SinA}=\dfrac{b}{SinB}=\dfrac{c}{SinC}\ \ \ \implies\ \ \dfrac{b+1}{2SinC*CosC}=\dfrac{b}{SinC*(4Cos^2C - 1)}=\dfrac{b-1}{SinC}.\\ Multiplying\ each\ term\ by\ SinC,\ \ \ \ \boxed{1} \dfrac{b+1}{2*CosC}=\boxed{2}\dfrac{b}{4Cos^2C - 1}=\boxed{3}\dfrac{b-1} 1.\\ Using\ dividendo-componendo,\ \boxed{3}+\boxed{2},\ \ \boxed{1} \dfrac{b+1}{2*CosC}=\boxed{3}+\boxed{2},=\dfrac{2b - 1}{4Cos^2C}.\\ \implies\ \dfrac{4Cos^2C}{2*CosC}=\dfrac{2b - 1}{b+1},\ \ \ \ \therefore\ simplifying.\ \ CosC=1-\dfrac 3{2*(b+1)}...(**)\\$ $Substituting\ {**} \ in\ \boxed{1}\ and\ equating\ with\ \boxed{2},\ \ \ \dfrac{b+1}{2*(1 - \frac 3{2*(b+1)})}=b - 1.\\ \implies\ \dfrac{(b+1)^2}{2b - 1}=b-1.\ \ \ b\neq0,\ \therefore\ simplifying\ \ b=5.\\$ $(a,b,c,)=(4,5,6). \ \ So\ the\ sum\ of\ their\ squares\ is =16+25+36=\ \ \ \large\ \color{#D61F06}{77}$

i) Let the 3 sides of the triangle be n, n+1, n+2 where n is a natural number; and let the smallest be α deg; so biggest angle is 2α deg and the 3rd angle would be (180 - 3α).

ii) Applying sine law of the triangle, we have n/sin(α) = (n+1)/{sin(180 - 3α) = (n+2)/sin(2α)

==> n/sin(α) = (n+1)/sin(3α) = (n+2)/2 sin(α) cos(α)

==> n/sin(α) = (n+1)/{3sin(α) - 4sin³α} = (n+2)/2 sin(α) cos(α) ² ³

Multiplying by sin(α), as α is not equal to 0, sin(α) is also not equal to zero

n = (n+1)/(3 - 4sin²α) = (n+2)/2*cos(α)

iii) From the above n/(n + 1) = 1/(3 - 4sin²α) = 1/(4cos²α - 1) ==> cos²α = (2n + 1)/4n ----- (1)

and n/(n + 2) = 1/{2*cos(α)} ==> cos(α) = (n + 2)/2n ==> cos²α = (n + 2)²/4n² ----- (2)

iv) Equating (1) & (2): (2n + 1)/4n = (n + 2)²/4n² ==>n² - 3n - 4 = 0 Solving either n = 4 or -1 But being n is a natural number n is not equal to -1;hence n = 4

Thus the measure of 3 sides are 4, 5 & 6 units. Sum of squares: 77