Can you handle imaginary numbers?
Algebra
Level
pending
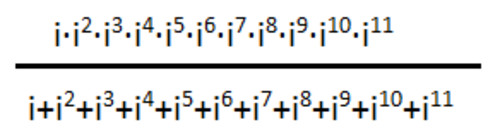How does multiplication over addition imply over imaginary numbers?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Since i=i, i^2= -1, i^3=-i and i^4=1, then the product of i, i^2, i^3 and i^4 is equal to -1. The same pattern with the next 4 imaginary numbers. Hence, i...i^8 is equal to positive one. Note that i^9, i^10 and i^11 is equal to -1. Then the numerator comes up with -1.
The denominator deals with addition. Since you already know the values, the sum of i, i^2, i^3 and i^4 is equal to 0. The same as the next 4 imaginary numbers. But note that i^9 is equal to i; i^10 is equal to -1; and i^11 = -i. Then, it's sum will be -1.
-1 divided by -1 is a positive 1. :D