Can you integrate?
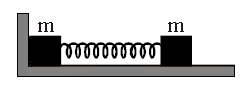 Let us name the block on the left as A and block on the right as B. Blocks A and B of mass
m
are connected to a spring of spring constant
k
. If B is displaced left by distance
x
and released at time
t
=
0
, Find the value of
∫
0
∞
N
d
t
Where
N
is the normal force applied by the vertical wall. Give your answer in SI units.
Let us name the block on the left as A and block on the right as B. Blocks A and B of mass
m
are connected to a spring of spring constant
k
. If B is displaced left by distance
x
and released at time
t
=
0
, Find the value of
∫
0
∞
N
d
t
Where
N
is the normal force applied by the vertical wall. Give your answer in SI units.
Note: Take m = 1 kg , k = 2 5 N/m , x = 7 0 cm . And assume all surfaces are smooth. Also assume the horizontal surface to be infinitely long .
The answer is 3.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is how I did,
The velocity of the COM when the Normal reduces to 0 is 2 v
So total change in momentum = ∫ 0 ∞ N . d t = 2 m × ( v − 2 v ) = m v = 3 . 5 .
Here v can be easily found out using 2 1 k x 2 = 2 1 m v 2
⟹ v = x k m
⟹ v = 5 x
So we put value and get ∫ 0 ∞ N . d t = 3 . 5 k g m s − 1
All we have to do is find the change in momentum
Clearly, what we need to find is the final momentum of the two block system as only normal force (by vertical wall) is the cause for change in momentum for the two block system. The momentum of the system will not change after A looses contact with the wall. Hence to find the final momentum of the system let us consider the moment just after A loses contact with the ball At that instant there will be almost negligible elongation on the spring (think why?). speed of A would be zero. Let the speed of B be v. and hence from energy conservation, 2 1 m v 2 = 2 1 k x 2 Hence final momentum = mv
Hence the value of the integral is k m x .