Can you measure the angle?
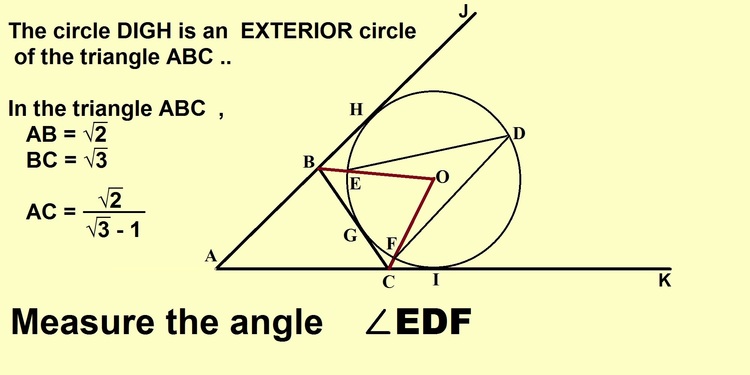 According to the picture above , what is the measure(in degrees) of ∠EDF ?
(consider 'O' as the center of the circle DIGH)
According to the picture above , what is the measure(in degrees) of ∠EDF ?
(consider 'O' as the center of the circle DIGH)
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
it is something very interesting to solve that by guessing what an angle it can be..
By Law of Cosines on △ A B C , ( 3 − 1 s q r t 2 ) 2 = ( 2 ) 2 + ( 3 ) 2 − 2 ⋅ 2 ⋅ 3 cos B
Simplifying ths expression, we obtain that 2 + 3 = 5 − 2 6 cos B
Isolating cos B shows that cos B = 2 6 3 − 3 = 4 6 − 2 so B = 7 5 ∘ .
By Law of Sines, sin 7 5 ∘ 3 − 1 2 = sin C 2 Solving for sin C , we obtain sin C = 2 2 so C = 4 5 ∘ . This also means A = 6 0 ∘ .
Note that B O is the angle bisector of ∠ C B J , and C O is the angle bisector of ∠ B C K , from the definition of the excircle. Thus, ∠ B C O = 2 1 3 5 and ∠ B C O = 2 1 0 5 .
Thus, ∠ B O C = 6 0 ∘ , and ∠ E D F = 2 6 0 = 3 0 ∘ .
Using Heron's formula we get the area of triangle 1.183012702,Now 1/2 * BC * AC sin C=1.183..... solving it we get C=45,and the same way B=75,So JBC=105 that makes OBC=105/2=52.5[when an exterior circle is drawn the exterior angle is bisected] ,similarly OCB=67.5,then BOC=60,and inscribed is 1/2 of central angle so EDF=60/2=30
L e t , i n t r i a n g l e A B C , B C = a = 3 , A C = b = 3 − 1 2 , & A B = c = 2 s o , C o s ∠ A B C = 2 c a c 2 + a 2 − b 2 = 2 × 2 × 3 ( 2 ) 2 + ( 3 ) 2 − ( 3 − 1 2 ) 2 = 4 6 − 2 s o , ∠ A B C = cos − 1 ( 4 6 − 2 ) = 7 5 & ∠ J B C = ( 1 8 0 − 7 5 ) = 1 0 5 C o s ∠ A C B = 2 a b a 2 + b 2 − c 2 = 2 × 3 × ( 3 − 1 2 ) ( 3 ) 2 + ( 3 − 1 2 ) 2 − ( 2 ) 2 = 2 1 s o , ∠ A C B = cos − 1 ( 2 1 ) = 4 5 & ∠ K C B = ( 1 8 0 − 4 5 ) = 1 3 5 A s c i r c l e D I G H i s a n e x t e r i o r c i r c l e , s o B O & C O a r e t h e b i s e c t o r s o f ∠ J B C & ∠ K C B s o , ∠ O B C = 2 ∠ J B C = 2 1 0 5 = 5 2 . 5 & ∠ O C B = 2 ∠ K C B = 2 1 3 5 = 6 7 . 5 I n t r i a n g l e O B C , ∠ B O C = 1 8 0 − ∠ O B C − ∠ O C B = 1 8 0 − 5 2 . 5 − 6 7 . 5 = 6 0 s o , ∠ E O F = ∠ B O C = 6 0 a s w e k n o w , a n i n s c r i b e d a n g l e i s h a l f o f t h e c e n t r a l a n g l e f r o m t h e s a m e a r c ( i n t e r c e p t e d a r c ) s o , ∠ E D F = 2 ∠ E O F = 3 0
We know that ∠ B O C = 9 0 ∘ − 2 ∠ A .
Applying Law's of cosine in △ A B C , We have B C 2 = A C 2 + A B 2 − 2 × A C × A B × cos ∠ A .
Substituting the values we get cos ∠ B A C = 2 1 .
Hence ∠ A = 6 0 ∘ .
Therefore, ∠ B O C = 9 0 ∘ − 2 6 0 ∘ = 9 0 ∘ − 3 0 ∘ = 6 0 ∘ .
Therefore, ∠ E D C = 2 1 × 6 0 ∘ = 3 0 ∘