Can You Minimize This?

The formula for the distance in question, $d$ can be found here . That is, for triangle with side lengths $a,b,c$ and angles $A,B,C$ , respectively, we want to minimize $\left( {\dfrac{9c^2}{4\sin^2 C} - (a^2 + b^2 + c^2) } \right)^{1/2}$ which is the same thing as minimizing the square of the distance, $D := \dfrac{9c^2}{4\sin^2 C} - (a^2 + b^2 + c^2)$ . $$ Without the loss of generality, let $a=1,b=3$ and $c$ denote the unknown side length. By triangle inequality , $3-1 < c < 3 + 1$ or $2<c<4$ . Thus, we have a single variable function $D(c) = \dfrac{9c^2}{4\sin^2 C} - c^2 - 10$ Using cosine rule , we have $c^2 = 1^2 + 3^2 -2\cdot1\cdot3 \cdot \cos C \quad \Leftrightarrow \quad 2\cos C = \dfrac{10-c^2}3$ Since $4 \sin^2 C = 4 - 4\cos^2 C$ , then $4\sin^2 C = 4 - (2\cos C)^2 = 4 - \left( \dfrac{10-c^2}3 \right)^2$ Substitute the expression into $D(c)$ and simplify gives: $D(c) = - \dfrac{81c^2}{c^4 - 20c^2 + 64} -c^2 - 10, \quad\quad 2<c<4$ For simplicity sake, let $c^2 = x$ with $4 <x<16$ , we want to minimize $\begin{array} { r c l } f(x) &:=& - \dfrac{81x}{x^2-20x + 64} - x - 10 \\ \phantom0\\ &=& -x - \dfrac{108}{x-16} + \dfrac{27}{x-4} - 10, \quad \quad 4<x<16 \end{array}$ At its critical point, $f'(x) = 0$ , which is $- \dfrac{27}{(x-4)^2} + \dfrac{108}{(x-16)^2} - 1 = 0 \quad \Leftrightarrow\quad \dfrac{(x^2-35x+232)(x^2-5x+40)}{(x-16)^2 (x-4)^2 } = 0$ Using the quadratic formula with the constraint $4<x<16$ , we have a critical point $x = \dfrac{35 - 3\sqrt{33}}2$ . $$ Since both $\lim \limits_{x\to4^+} f(x)$ and $\lim \limits_{x\to16^-} f(x)$ diverge to infinity, this means that $f(x)$ have no maximum value, and thus the critical point we've found is a minimum value. Hence, the miminum value of $D(c)$ occurs when $c = \sqrt{x} = \sqrt{ \frac{35-3\sqrt{33}}2 }$ , $d = \sqrt{\min(D)} = \sqrt{D\left ( \sqrt{ \frac{35-3\sqrt{33}}2 } \right )} =\sqrt{\dfrac{33\sqrt{33}-175}8} \approx 1.3495632.$ The answer is $\lfloor 10^5 \cdot 1.3495632 \rfloor =\boxed{134956} .$

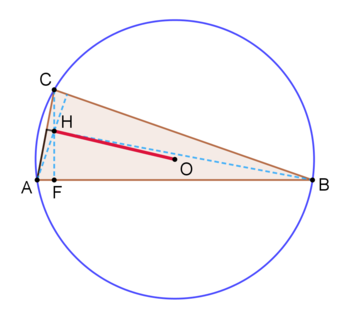This is the triangle with HO minimised

A convenient formula for the distance $d$ between the orthocentre $H$ and the circumcenter $O$ of a triangle is

$HO=\frac{\sqrt{{{a}^{6}}-{{b}^{2}}{{a}^{4}}-{{c}^{2}}{{a}^{4}}-{{b}^{4}}{{a}^{2}}-{{c}^{4}}{{a}^{2}}+3{{b}^{2}}{{c}^{2}}+{{b}^{6}}-{{b}^{2}}{{c}^{4}}-{{b}^{4}}{{c}^{2}}}}{4\Delta }$ where $a$ , $b$ and $c$ are the side lengths of the triangle and $\Delta$ is its area. This formula can be found here .

Let $a=1$ and $b=3$ . Then combined with Heron's formula for the area, the above formula gives $d=HO=\frac{\sqrt{{{c}^{6}}-10{{c}^{4}}-55{{c}^{2}}+640}}{\sqrt{-{{c}^{4}}+20{{c}^{2}}-64}}$ Minimising $d$ is equivalent to minimising ${{d}^{2}}$ i.e. we are looking for the minimum of the function $f\left( c \right)=\frac{{{c}^{6}}-10{{c}^{4}}-55{{c}^{2}}+640}{-{{c}^{4}}+20{{c}^{2}}-64c}$ , where $c\in \left( 2,\ 4 \right)$ (a restriction imposed by the triangle inequality).

Taking the derivative,

${f}'\left( c \right)=-\frac{2c\left( {{c}^{8}}-40{{c}^{6}}+447{{c}^{4}}-2560{{c}^{2}}+9280 \right)}{{{\left( -{{c}^{4}}+20{{c}^{2}}-64c \right)}^{2}}}$

At the critical point

$\begin{aligned} {f}'\left( c \right)=0 & \overset{c\ne 0}{\mathop{\Leftrightarrow }}\,{{c}^{8}}-40{{c}^{6}}+447{{c}^{4}}-2560{{c}^{2}}+9280=0 \\ & \Leftrightarrow \left( {{c}^{4}}-35{{c}^{2}}+232 \right)\left( {{c}^{4}}-5{{c}^{2}}+40 \right)=0 \\ & \Leftrightarrow {{c}^{4}}-35{{c}^{2}}+232=0 \\ & \overset{2<c<4}{\mathop{\Leftrightarrow }}\,c=\sqrt{\frac{35-3\sqrt{33}}{2}} \\ \end{aligned}$

At this point, the second derivative is positive, ensuring that we have a minimum, which is $f\left( \sqrt{\frac{35-3\sqrt{33}}{2}} \right)=\frac{33\sqrt{33}-175}{8}$ Hence, the smallest possible distance between the orthocenter and circumcenter of our triangle is $d=\sqrt{\frac{33\sqrt{33}-175}{8}}\approx 1.3495632319$ For the answer, $\left\lfloor {{10}^{5}}d \right\rfloor =\boxed{134956}$ .

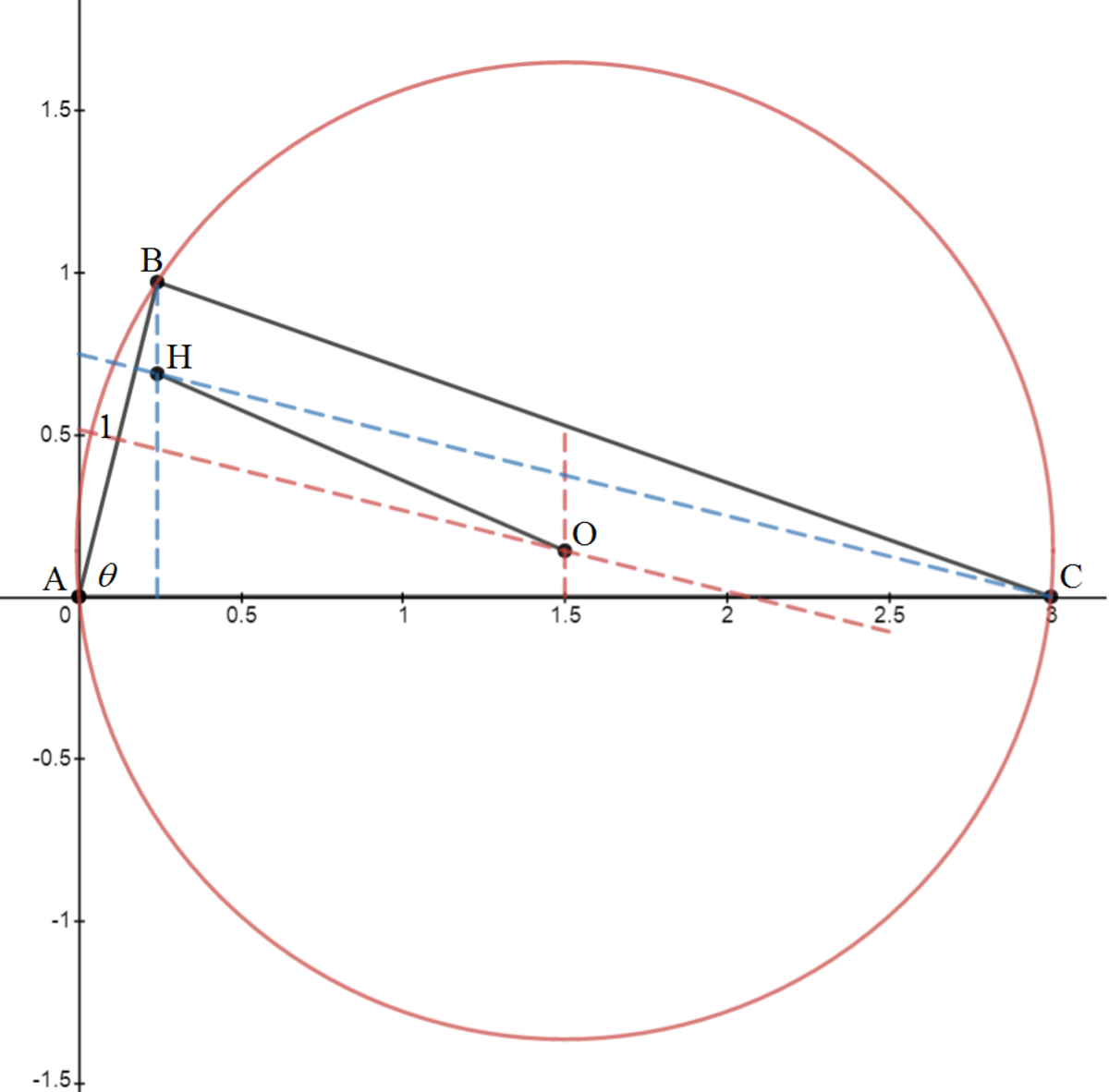
Label the triangle $ABC$ such that $AB=1$ and $AC=3$ . Let $A(0,0)$ and $\angle A = \theta$ . Then $B(\cos \theta, \sin \theta)$ and $C(3,0)$ . And the circumcenter $O(x_O, y_O)$ is the intersecting point of perpendicular bisectors of $AB$ and $AC$ . Therefore $x_O = \frac 32$ and

$\frac {y_O-\frac 12 \sin \theta}{x_O - \frac 12 \cos \theta} = - \cot \theta \implies y_O = \frac {\sin \theta - (3-\cos \theta)\cot \theta}2$

Then the circumcenter is $O \left(\dfrac 32, \dfrac {\sin \theta - (3-\cos \theta)\cot \theta}2 \right)$

The orthocenter $H(x_H, y_H)$ is the intersecting point of the altitudes from $A$ and $C$ . Then $x_H = \cos \theta$ and

$\frac {y_H}{x_H-3} = - \cot \theta \implies y_H = (3-\cos \theta)\cot \theta$

Then the orthocenter is $H \left(\cos \theta, (3-\cos \theta) \cot \theta \right)$ .

Therefore $OH = \sqrt{\left(\dfrac 32-\cos \theta \right)^2+\left(\dfrac {\sin \theta - 3(3-\cos \theta) \cot \theta}2\right)^2}$ . Finding the minimum of $OH$ numerically, we have $d \approx 1.349563232 \implies \lfloor 10^5d \rfloor = \boxed{134956}$ .