Can You Pivot 2?
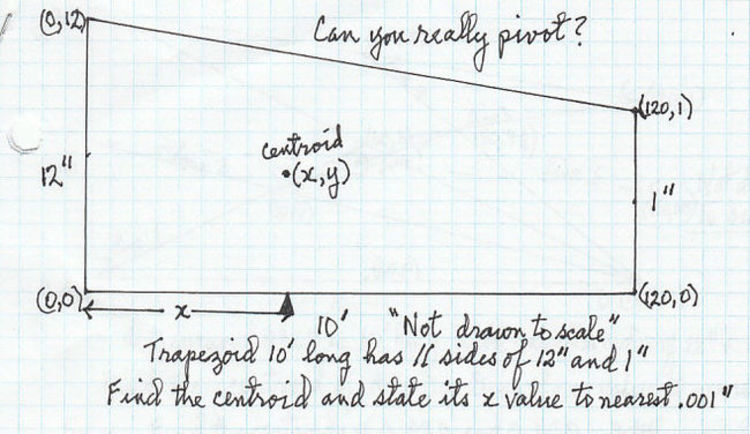A trapezoid 10' long with parallel sides of 12" and 1" is drawn on a coordinate plane with one corner on the origin and 2 sides placed on the
x
and
y
axis.
Find the centroid of the trapezoid and state the x value of the centroid to the nearest .001 inch.
The answer is 43.077.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Soln
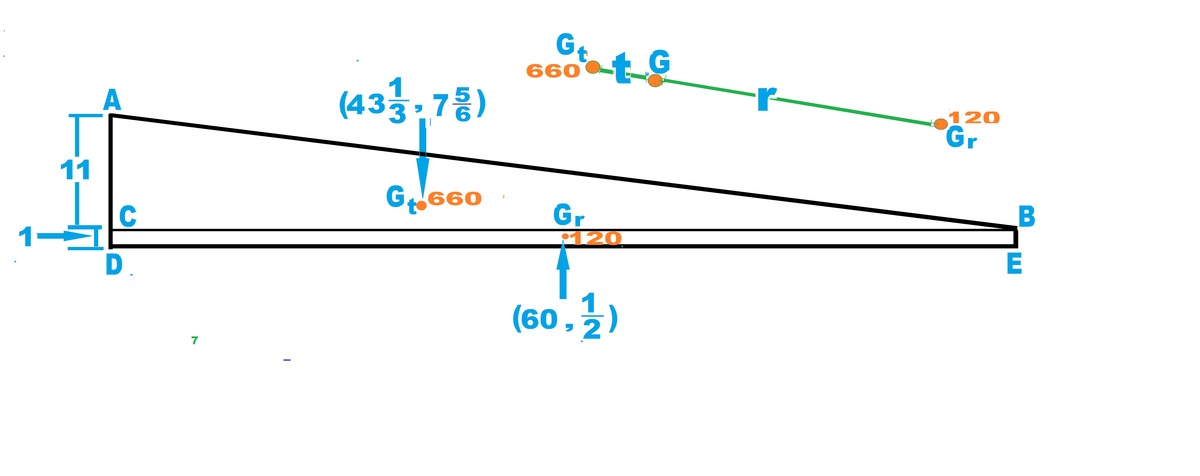Trapezoid ABCDE is made up of a triangle ABC and a rectangle BCDE.
Area of ABC=
2
1
∗
1
1
∗
1
2
0
=
6
6
0
,
t
h
a
t
o
f
B
C
D
E
=
1
∗
1
2
0
=
1
2
0
.
G
t
of triangle is one third from base.
So its horizontal distance from vertical side is
3
1
∗
1
2
0
=
4
0
,
a
n
d
f
r
o
m
H
o
r
i
z
o
n
t
a
l
s
i
d
e
3
1
1
But the horizontal side is y=1,
∴
G
t
(
4
0
,
3
1
1
+
1
)
⟹
G
t
(
4
0
,
3
1
4
)
.
Area of BCDE has its C.G. at its center, So
G
r
(
6
0
,
2
1
)
.
Let G be the C.G. of the trapezoid ABCDE. Considering horizontal components,
X
G
r
−
X
G
t
=
6
0
−
4
0
=
2
0
.
L
e
t
X
G
X
G
t
=
t
a
n
d
X
G
X
G
r
=
r
.
T
a
k
i
n
g
m
o
m
e
n
t
s
a
b
o
u
t
X
G
,
6
6
0
∗
t
=
1
2
0
∗
r
⟹
t
r
=
2
1
1
,
b
u
t
t
+
r
=
2
0
.
∴
t
=
2
0
∗
1
1
+
2
2
.
S
o
X
G
t
=
4
0
+
1
3
4
0
=
4
3
.
0
7
7
We can solve for the Y-component in the same way.