Can you reach your destination?
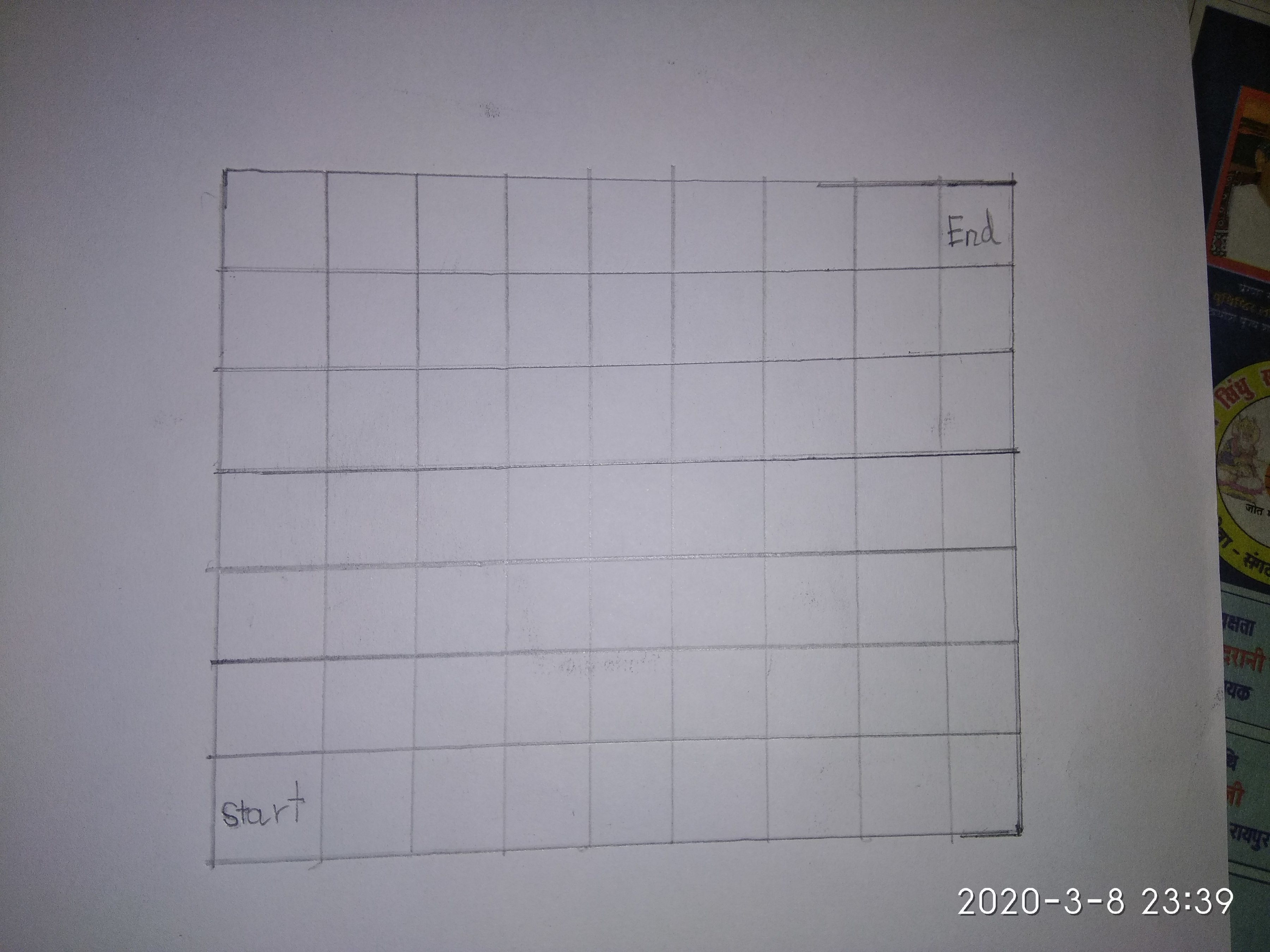
You are at the bottom left square of a 7 × 9 grid. In each turn , you can either move a square up , a square down or a square right . You cannot go back to the square you came from. You have to reach to the top right square. In how many ways can you do so? If your answer can be written as a b enter your answer as a + b .
All of my problems are original
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yes this is the case for column, and 7 9 is for the end point.
I meant to say that, 7 8 choices would be there, when we consider the object moving in columns (not on lines) because it will reach the last square way before. But if take points into consideration; suppose we took start point A and end point B (the opposite vertex of 9 × 7 rectangle ), then we would have exactly 7 9 choices.
Usually, these type of questions consider the object to be point...
Log in to reply
I want to know how you came up with 7 9 choices.
Log in to reply
When you move on lines from A , then you need to move 9 units horizontally and 7 units (having variable choices) vertically to reach the point B .
@Atomsky Jahid 9 points make 8 colunms (or spaces).
Once you move to a column, you can't go back. Now, in each column, you can move to 7 squares. Also, you have to go to every column. Therefore, it is similar to selecting a square from each column. Therefore, the answer is 7 × 7 × 7 ... ×7 = 7 8
You haven't clarified what you meant by 'selecting a square from each column'. I am assuming the square means the transition square through which you change your column (moving one square right).
Your reasoning is mostly correct. But, it doesn't apply to the last column. Let's say, we've selected the 5th square of the 8th column. So, when we move into the last column, the choice has already been made. Now, we can only go upwards to meet our end point. Therefore, no selection is going on for the last column.
The answer should be 7 8 .
Oh man, thanks. Can you please post it in report section so that brilliant community can change its answer?
Log in to reply
Ok, I've reported it. Hopefully, it gets fixed soon.
Log in to reply
Mention Calvin Lin sir to get it fixed sooner by using @
I am late to the discussion and do not know whether the answer has been changed. Just so I'm clear, what is the correct answer? Are we talking about an off-by-one error? Also, please provide a generalised formula in terms of rows and columns. Thank you!
Answer should be 1 5 . I didn't bsee the case he told me. In general for n rows and m columns, answer is n m − 1
We will approach this problem by considering the 'route through columns'.
In how many ways can we get to the second column? We can do it in 7 ways. In how many ways can we go to the third column from the second column? Also in 7 ways.
This goes on till the ninth column. And, the possible ways to go to the next column is always 7. Therefore, we need to count how many transitions we have to make to go to the ninth column. There are 8 such transitions. So, there are 7 8 ways to reach the end point.