Can You Solve a Magic Square?

Computer Science Level 5

Given above is a $4 \times 4$ grid. In how many ways can you fill numbers from 1 to 16 inclusive in each individual box of the above grid such that sum of numbers in all the rows, columns, and main diagonals are the same?

Details and Assumptions :

Main diagonals are the diagonals connecting the vertices of the grid.
For a grid to qualify, the sum of numbers in it's every row, column, and main diagonal must be the same. Sum of rows or columns or diagonals of two separate grids may not be the same.
Rotations and reflections of the grid don't count distinct.
Every digit from 1 to 16 inclusive must be used exactly once.
An explicit example of such grid -

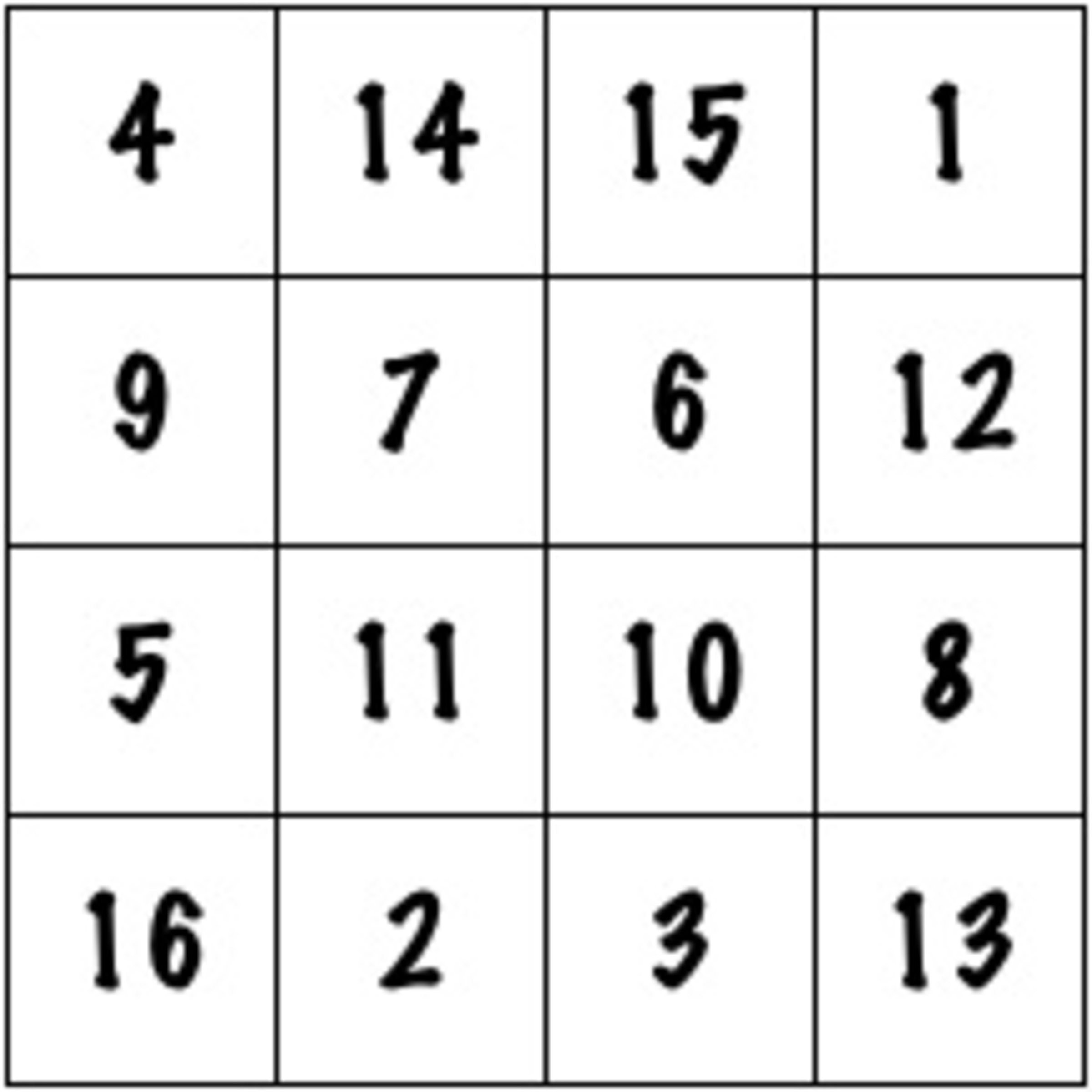
The answer is 880.

1 solution

David Hammond
Nov 9, 2019

# An Efficient Algorithm for Constructing all Magic Squares of
# Order Four
# @see https://pdfs.semanticscholar.org/dcdb/c3d9e7e31b14d9f9c1a94d4678258f077917.pdf

from itertools import permutations

N = 0

x = [0] * 16
for p in permutations(range(1, 17), 7):
  x[0] = p[0]
  x[1] = p[1]
  x[2] = p[2]
  x[4] = p[3]
  x[5] = p[4]
  x[6] = p[5]
  x[8] = p[6]

  x[3] = 34 - x[0] - x[1] - x[2]
  x[7] = 34 - x[4] - x[5] - x[6]
  x[9] = x[0] + x[4] + x[8] - x[3] - x[6]
  x[10] = (2*x[3] + x[6] + x[7] - 2*x[0] - x[4] - x[5] - 2*x[8] + 34)/2
  x[11] = x[0] + x[5] + x[10] - x[3] - x[7]
  x[12] = 34 - x[0] - x[4] - x[8]
  x[13] = 34 - x[1] - x[5] - x[9]
  x[14] = 34 - x[2] - x[6] - x[10]
  x[15] = 34 - x[3] - x[7] - x[11]

  if sum([i > 0 and i < 17 for i in x]) == 16:
    if len(set(x)) == 16:
      N = N + 1
      print(N, x)

print(N / 8) # 8 rotations + reflections

Can You Solve a Magic Square?

The answer is 880.

1 solution

0 pending reports