Can you solve the angles
The diagram below shows a series of 2019 squares with side lengths of 1 where:
- 2019 lines are drawn from to , , ......, .
- On line , there are 2016 points labeled , from to , where = , and 2016 lines are drawn from to , , , ... , .
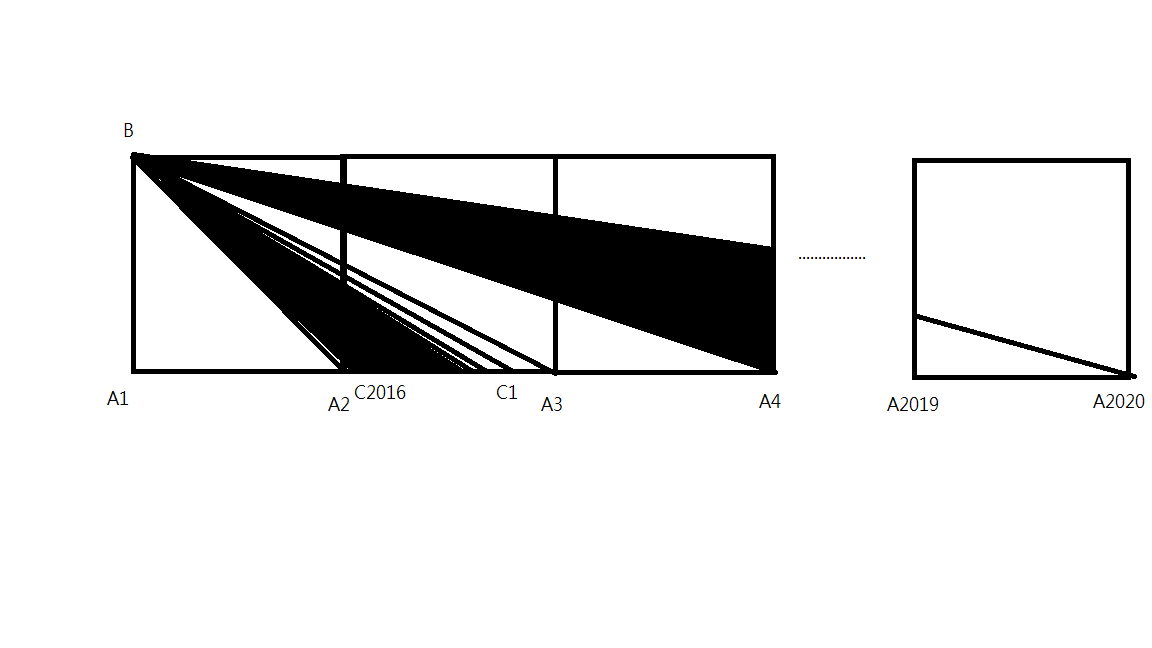 (Diagram not drawn to scale)
(Diagram not drawn to scale)
Evaluate the following in degrees.
+
The answer is 90810.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First let's solve ∠ B A 2 A 1 + ∠ B A 3 A 2 + ∠ B A 4 A 3 .
We know ∠ B A 2 A 1 = 4 5 ∘ , since ∠ B A 1 A 2 = 9 0 ∘ and A 1 B = A 1 A 2 = 1 .
In △ B A 2 A 3 and △ B A 4 A 2 :
B A 2 = 2 , A 2 A 4 = 2
∵ B A 2 A 2 A 3 = A 2 A 4 B A 2 = 2 1
∠ B A 2 A 3 = ∠ A 4 A 2 B
∴ △ B A 2 A 3 ∼ △ A 4 B A 2 ( S A S )
∴ ∠ B A 4 A 3 = ∠ A 3 B A 2
∴ ∠ B A 3 A 2 + ∠ B A 4 A 3 = ∠ B A 3 A 2 + ∠ A 3 B A 2 = ∠ B A 1 A 2 = 4 5 ∘
What pattern are we trying to prove?
You'll find that △ B A 2 C n ∼ △ A n + 4 A 2 B and here's why:
In △ B A 2 C n and △ B A 2 A n + 4 :
A 2 C n = A 2 A 3 − A 3 C n = 1 − n + 2 n = n + 2 2
A 2 A n + 4 = n + 4 − 2 = n + 2
∵ A 2 C n ⋅ A 2 A n + 4 = n + 2 2 ⋅ ( n + 2 ) = 2 = 2 ⋅ 2 = B A 2 2
∠ B A 2 C n = ∠ A n + 4 A 2 B
∴ B A 2 A 2 C n = A 2 A n + 4 B A 2
∴ △ B A 2 C n ∼ △ A n + 4 A 2 B
∴ ∠ B A n + 4 A 2 = ∠ C n B A 2
∴ ∠ B C n A 2 + ∠ B A n + 4 A 2 = ∠ B C n A 2 + C n B A 2 = ∠ B A 2 A 1 = 4 5 ∘
You'll notice that this actually is what the question is constructed of:
We have already proven that ∠ B A 2 A 1 + ∠ B A 3 A 2 + ∠ B A 4 A 3 = 9 0 ∘
We also have the formula ∠ B C n A 2 + ∠ B A n + 4 A 2 = 4 5 ∘
The rest can be rearranged to get ( ∠ B C 1 A 2 + ∠ B A 5 A 2 ) + . . . . . . + ( ∠ B C 2 0 1 6 A 2 + ∠ B A 2 0 2 0 A 2 ) = ( 4 5 × 2 0 1 6 ) ∘ = 9 0 7 2 0 ∘ .
Then adding the previous 9 0 ∘ we get to our final answer:
9 0 7 2 0 ∘ + 9 0 ∘ = 9 0 8 1 0 ∘