Can you solve this ?
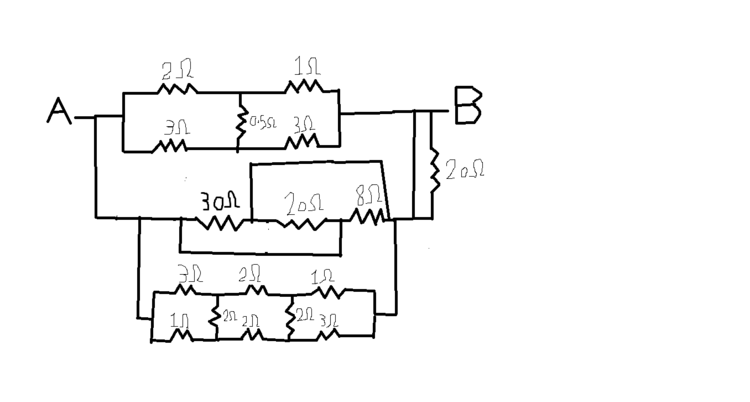
What is the equivalent resistance between A and B in this circuit?
Note: Approach to the nearest tenth.
The answer is 0.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I didn't get why there is no potential difference in the arm containing 0.5 Ohms resistor? We get 1.9591 to be the equivalent resistance of the top block and not 3. Which, as Tom said adds up to 0.914 in the final answer.
Log in to reply
when i was drawing this circuit i didn't notice that the ratios don't equal to each other i'm sorry about that i just wanted to collect all the tricky things that may face anyone during solving equivalent resistance problem in one problem.
I think there is a potential difference over the 0.5 ohm resistor in the upper section.
I calculate it to be 3/49 Volts with a test source of 1 Amp between A and B. Moreover, using Kirchoff's rules I get an equivalent resistance of 96/49 ohms, which comes very close to your solution and gives an equivalent resistance for the whole setup of 0.914 in stead of your 0.923 ohms (which off course rounds to the same).
Another reason why there is current through the 0.5 ohm resistor : if it was balanced, it was a balanced Wheatstone bridge and that means the ratio of the resistors in both branches should be equal, which isn't (1 <> 1/2)
Log in to reply
when i was drawing this circuit i didn't notice that the ratios don't equal to each other i'm sorry about that i just wanted to collect all the tricky things that may face anyone during solving equivalent resistance problem in one problem.
Log in to reply
Your combination of tricky things Enabled me to solve a problem of David Mattingly sir. I was struggling with that for about a month! Thanks!!!.....
I typed 0.96 .... it showed wrong .... bad luck
Log in to reply
I did the same mistake until i saw the note.
I wrote a note
.96 why wrong
Log in to reply
i wrote a note in the question if u read the question carefully ( u should approach to the nearest tenth)
answer is 1.7. PLS correct it
4 9 9 6 // 5 2 4 // 3 8 = 3 5 3 2 = 0.9142857142857142857142857142857+ = 0.9 {To the nearest tenth.}
Answer: 0 . 9
I got the answer as 4 2 5 5 3 8 7 2 o h m s instead of 1 3 1 2 o h m s using the same star-delta transformation. The answer was correct but if you could please tell me where I was wrong in method.
The resistance of the top branch was 4 . 8 o h m s , the middle one 4 6 1 2 1 o h m s and the bottom most branch as 4 6 9 6 o h m s .
Log in to reply
4.8 Ω is 5 2 4 Ω of the middle;
4 6 1 2 1 Ω is slightly incorrect from 3 8 Ω for the bottom;
4 6 9 6 Ω is slightly incorrect from 4 9 9 6 Ω for the top branch.
Overall is 3 5 3 2 Ω but not 1 3 1 2 Ω and neither 4 2 5 5 3 8 7 2 Ω . How could you get the order of resistances all swapped?
I think the resistance is 3 5 3 2 Ω rather than 1 3 1 2 Ω .
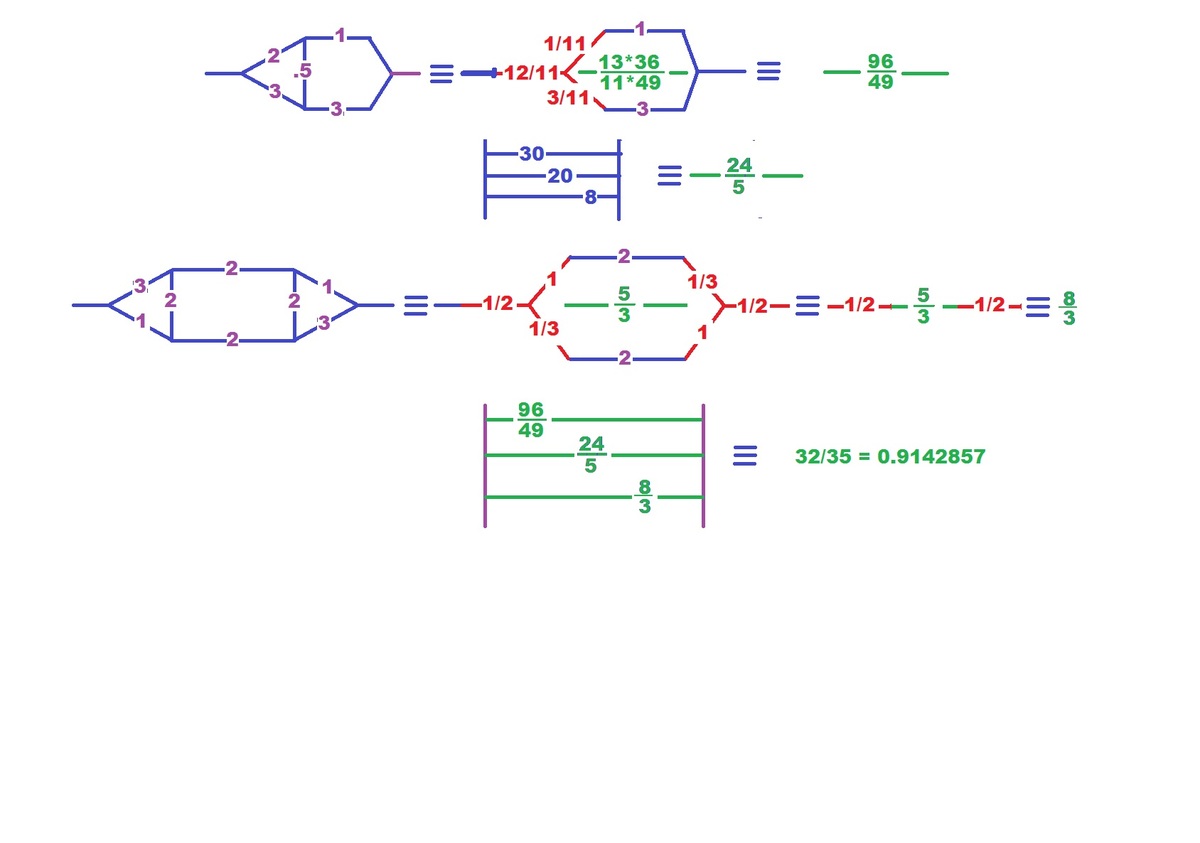
I used the same method. the first branch I got 96/49.
2
0
Ω
i
s
s
h
o
r
t
e
d
.
The top 2, 3, 0.5 Delta = 12/11, 2/11, 3/11 Star.
Solving the parallel branches with 12/11 in series, =96/49.
Middle are simple parallels,30, 20, 8 =24/5
Bottom 3, 1, 2 Delta is 1/2, 1, 1/3 star on first and third Deltas,
and then can be easily solved to 8/3.
Finally 96/49. 4.8, and 8/3 in parallel gives 0.9142857143.
We have one resistance should be neglected is 20 ohms in the right of the circuit because the current can pass in the wire which doesn't have any resistance.
Now we can divide this circuit into three other circuits the first is on the top ,, the second in the middle and the third on the bottom ,,
The top circuit has 2 squares the first and the third is delta connection by transforming them into star connection,, it will be solved,, The transformations laws in this link (The equivalent resistance of the top circuit approximately equals to 2 ohms).
The middle circuit has three resistances: 30 ohms , 20 ohms and 8 ohms resistances are parallel with each other (The equivalent resistance of the middle circuit is 4.8 ohms).
The bottom circuit has 3 squares the first and the third is delta connection by transforming them into star connection,, it will be solved,, The transformations laws in this link (The equivalent resistance of the bottom circuit is 8/3 ohms).
The three circuits are parallel and by adding them using Kirchoff´s Circuit Laws (The final equivalent resistance will be 12/13 ohms which is approximately equivalent to 0.9 ohms)