But graphing is so much easier!

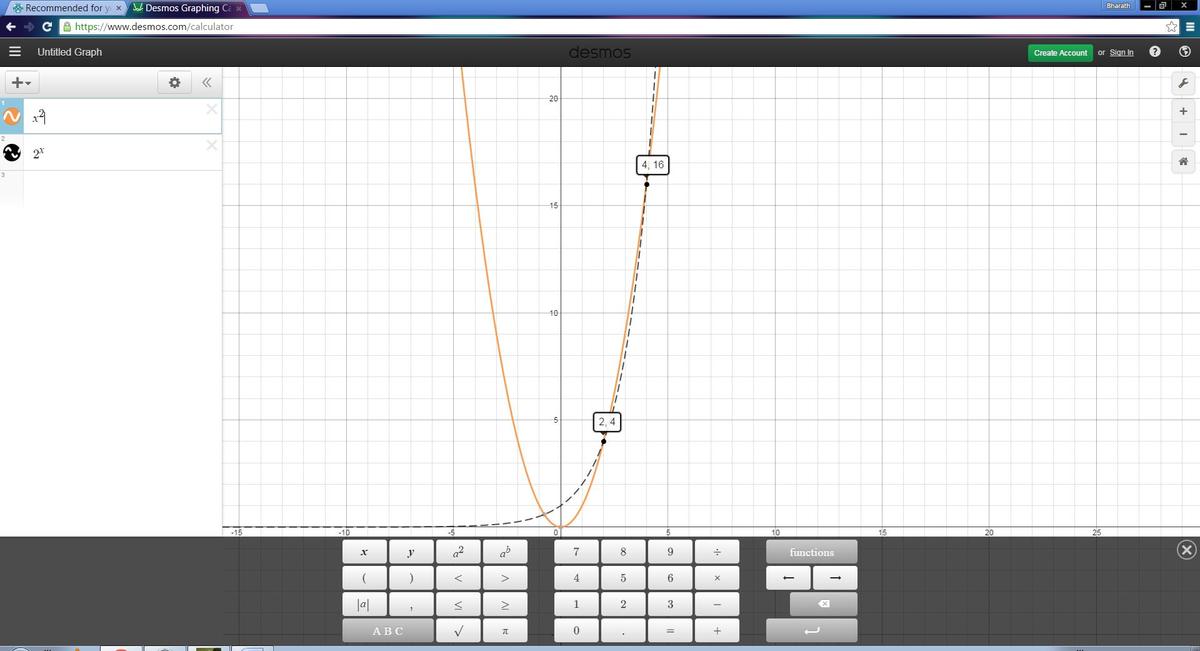
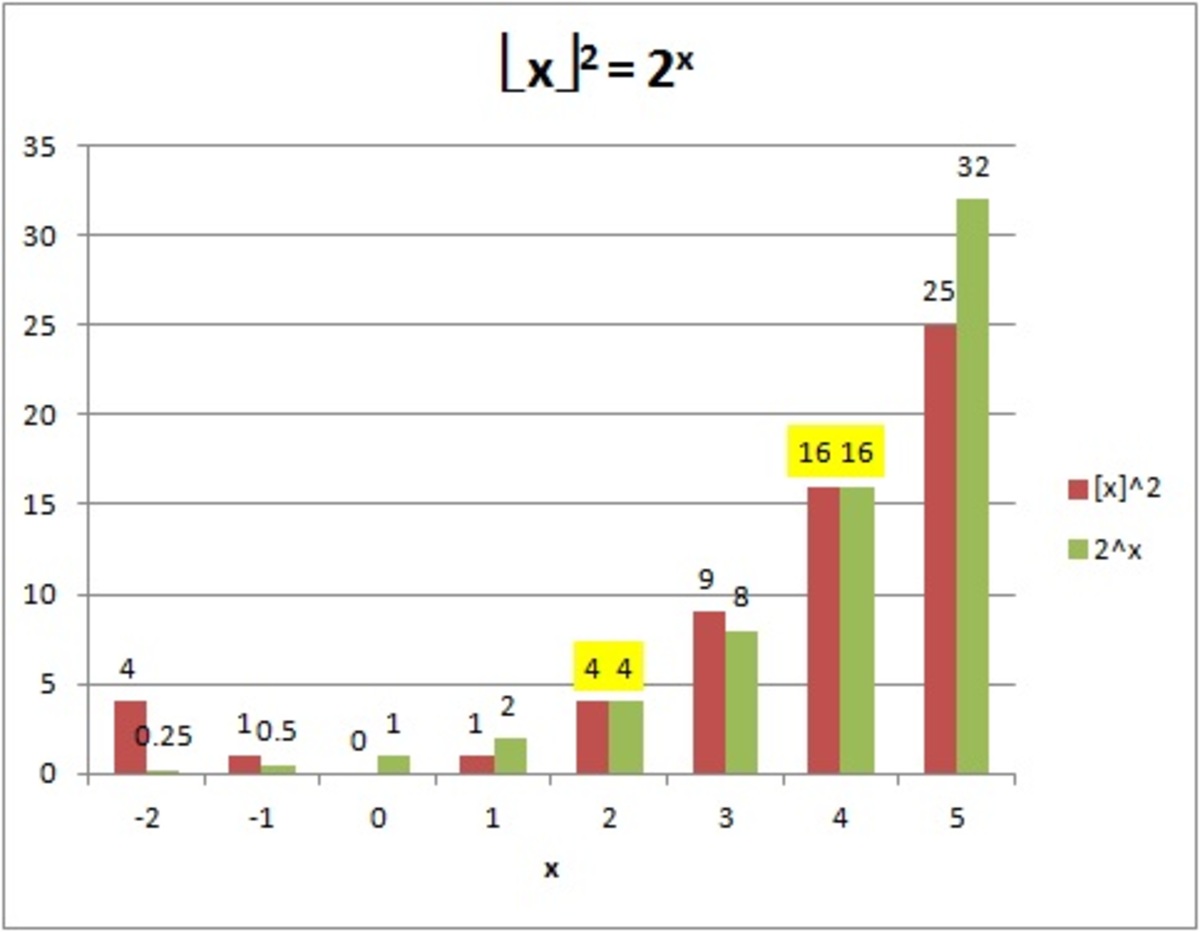
Since ~\lfloor x\rfloor~ is~ an~ integer,~ 2^x~must~be~also~an~integer.\therefore x\in~{\Large Z} \\\text{Since RHS is power of 2, LHS also must be multiple of 2 ONLY.}\\Let~k~\in~{\Large Z}^+ \text{ So x=2^k. Thus the equality becomes } (2^k)^2={\large 2^{2^k} } \\\therefore \text{equation is true only iff } 2k=2^k.\\\text{ONLY possible for } k=1~~and~~k=2.~~~\implies~~ x=2~~ or~~ 4.\\ \text{Putting floor on x does not seem to be of any use. }

Since we have to look for the integral solutions, $\lfloor x\rfloor = x$ . Hence we have to find the number of solutions to $\displaystyle x^2 = 2^x$ .

The graphs give the only solutions to be $\boxed{x= 2, 4}$

A graphs of $\lfloor x \rfloor ^2$ and $2^x$ for integer values of $x$ is plotted and shown above. It can be seen that there are $\boxed{2}$ integer solutions, when $x=2$ and $x=4$ .