Can you solve using a single equation?
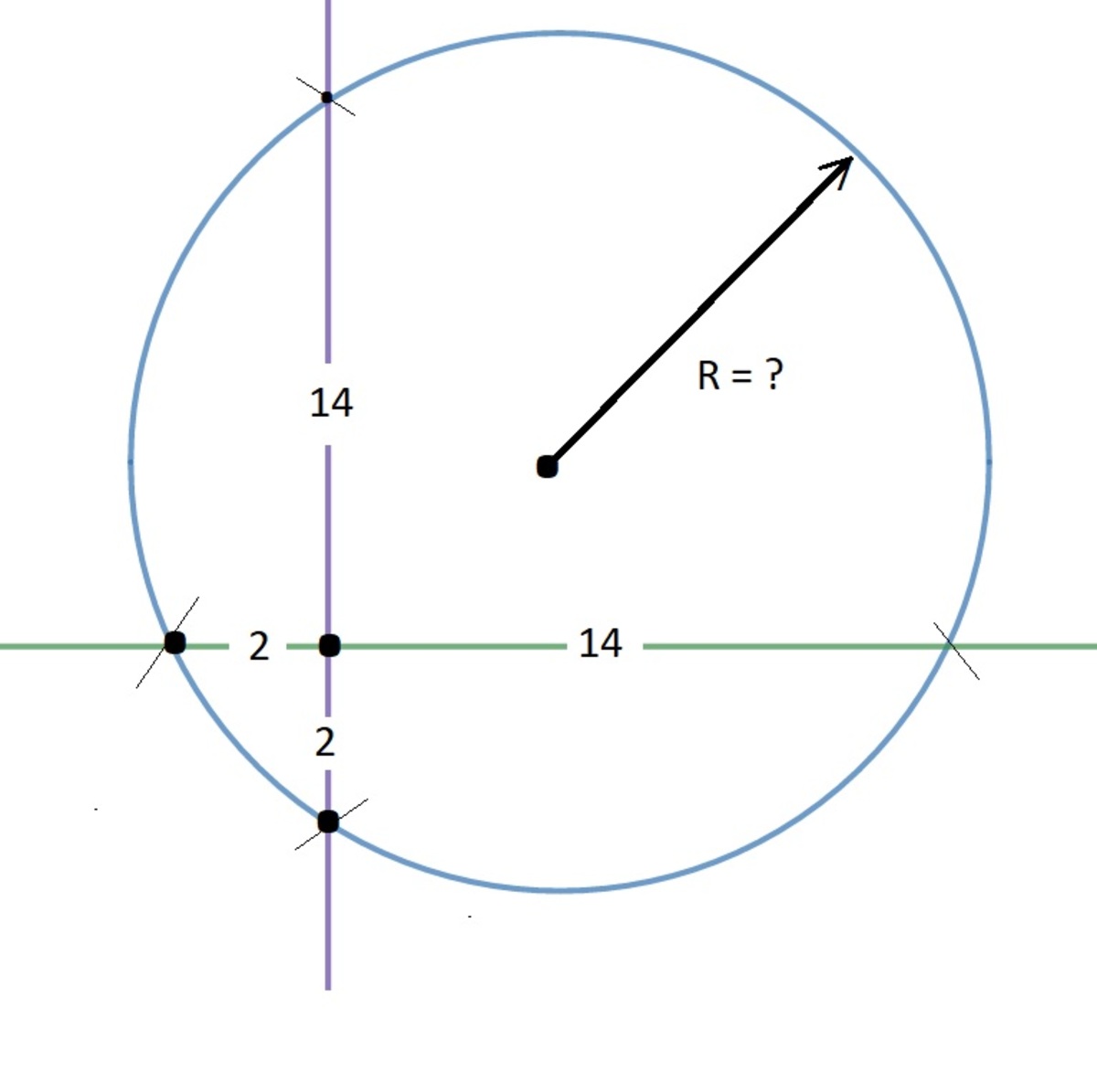 What is the value of the radius
R
?
What is the value of the radius
R
?
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
What is the origin as per your answer
The origin is the point ( 0 , 0 ) . :)
No, seriously. Two of the given points on the circle are ( − 2 , 0 ) and ( 1 4 , 0 ) . The perpendicular bisector of a line segment is the locus of points equidistant from the segment's endpoints (known theorem). It's pretty obvious that the midpoint is ( 6 , 0 ) and, since the segment is horizontal, the perpendicular must be vertical, hence it's the line x = 6 . The bisector of the segment between ( 0 , − 2 ) and ( 0 , 1 4 ) is deduced in the same way.
And any circle can be represented by the equation ( x − x 0 ) 2 + ( y − y 0 ) 2 = R 2 , where ( x 0 , y 0 ) is the centre of the circle and R is the radius. This is a direct consequence of Pythagoras' theorem.
If you look to see how the circle would have to shift to be centered on the origin we can see that it will need to shift 6 to the left and 6 down. Using this information we can show that the right triangle created using the radius and the shift of 6 and the remaining height of 8 creates a 3-4-5 triangle making the radius 10.
Label the points as follows:
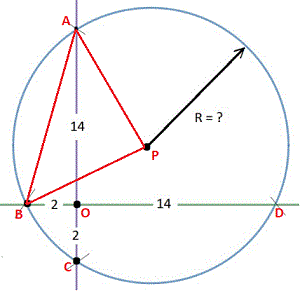
If two chords intersect in the interior of a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle. Therefore, ∠ A O B = 2 1 ( m A B + m C D ) = 9 0 ° . By symmetry, m A B = m C D , so that this solves to m A B = 9 0 ° . Since the measure of a minor arc is also defined as the measure of its central angle, ∠ A P B = m A B = 9 0 ° .
Therefore, △ A O B and △ A P B are right triangles sharing the same hypotenuse, so that by Pythagorean's Theorem, A B 2 = A O 2 + B O 2 = A P 2 + B P 2 , or
1 4 2 + 2 2 = 2 R 2
and this single equation solves to R = 1 0 .
Nice approach
But, it is not given that chords are perpendicular
Log in to reply
I believe the chords are to be assumed to be the x- and y-axes, which would make them perpendicular. That assumption probably needs to be stated in the problem itself, as it seems all other solutions use that assumption.
Is this a known theorem? Or have you derived it somehow?
Log in to reply
well it is a theorem but not that popular. It's even written on wikipedia's page about circles but that doesn't mean it's famous though.
Exactly, is it a standard theorem that can be applied in all cases?
Let the green and purple chords coincide with the x & y-axes respectively (such that their intersection point is the origin). Let the center of this circle be at the point ( α , β ) such that the required equation becomes ( x − α ) 2 + ( y − β ) 2 = R 2 . Substituting the four given circumferential points: ( x , y ) = ( 1 4 , 0 ) , ( − 2 , 0 ) , ( 0 , 1 4 ) , ( 0 , − 2 ) above yields the following system of equations:
( 1 4 − α ) 2 + ( 0 − β ) 2 = R 2 ;
( − 2 − α ) 2 + ( 0 − β ) 2 = R 2 ;
( 0 − α ) 2 + ( 1 4 − β ) 2 = R 2 ;
( 0 − α ) 2 + ( − 2 − β ) 2 = R 2
which ultimately produce the center point ( α , β ) = ( 6 , 6 ) and ( x − 6 ) 2 + ( y − 6 ) 2 = R 2 . Picking any one of the four given circumferential points finally produces R = 1 0 .
Draw two lines
connecting A : (-2,0) between B : (0,14) and B : (0,14) between C : (14,0)
and then use the law of sine:
AB/ sin(<BCA) = 2R
length of AB : root(14^2 + 2^2) = 10*root(2)
<BCA : pi/4
sin(<BCA) = 1/(root(2))
10*root(2)/{(1/(root(2))} =2R
=>R=10
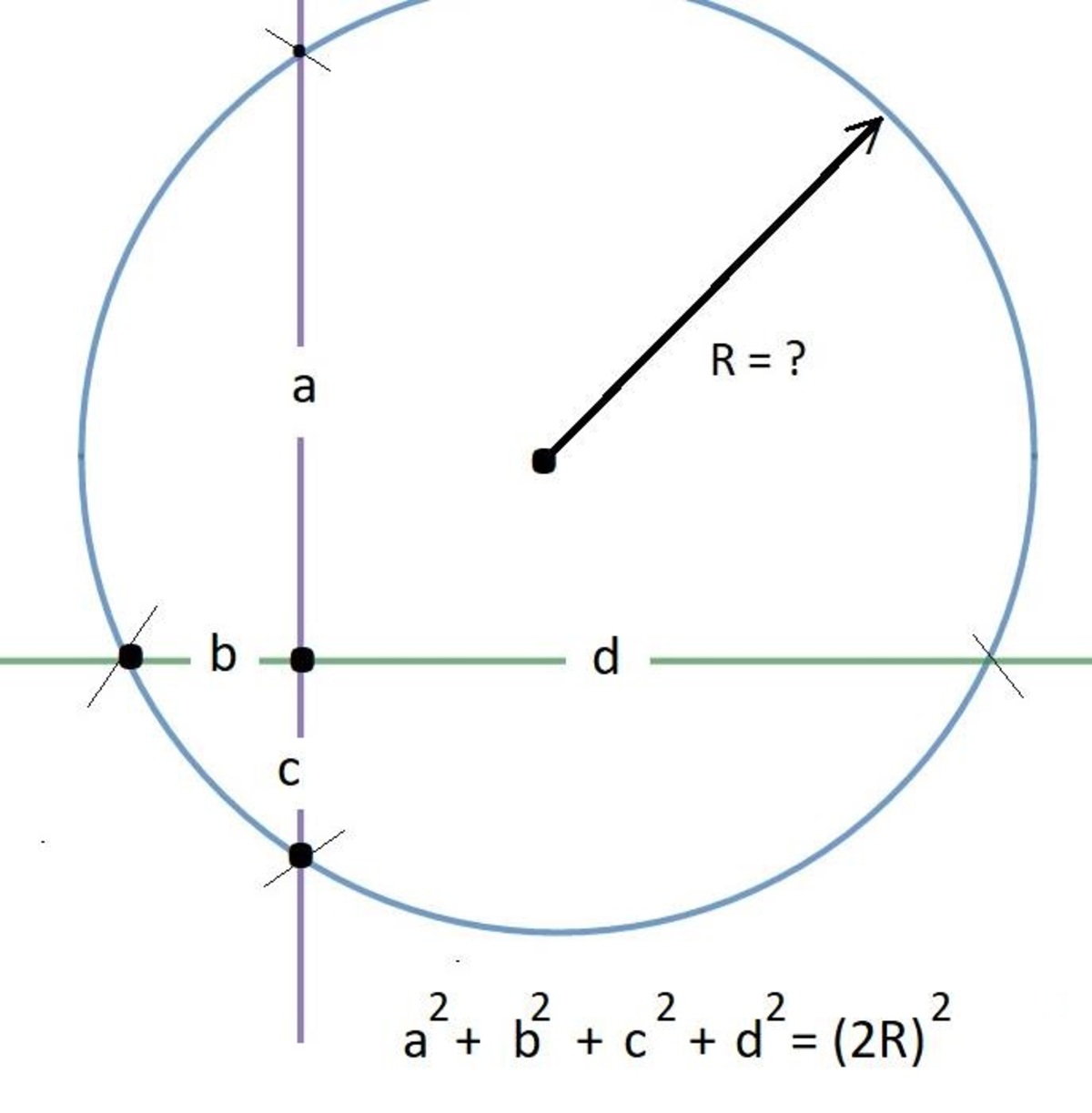
The centre must lie on the perpendicular bisectors of the two chords in order for it to be equidistant from the four given intercepts (from the basic definition of a circle, assuming this is indeed a circle).
The perpendicular bisectors are the lines x = 6 and y = 6 , hence the centre is ( 6 , 6 ) .
Thus we can write the equation of the circle thus: ( x − 6 ) 2 + ( y − 6 ) 2 = R 2 .
Substituting one of the intercepts: ( 1 4 − 6 ) 2 + ( 0 − 6 ) 2 = R 2 ⇒ 8 2 + 6 2 = R 2 ⇒ 1 0 0 = R 2 ⇒ R = 1 0 .