Can you stretch the boy?
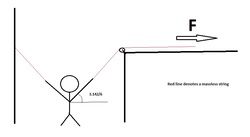 Find the magnitude of the force
F
required to fully stretch the boy's arms, i.e both his arms should make a right angle to the vertical.
Find the magnitude of the force
F
required to fully stretch the boy's arms, i.e both his arms should make a right angle to the vertical.
Note: The boy's mass is 50 kg and gravitational acceleration is g = 9 . 8 m/s 2 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
HAHA, sorry..
Just a heads up, but shouldn't
- T \sin \theta = mg
- T \cos \theta = F
Note that this doesn't cause any changes to the true answer, just trying to get the vectors right...
Simply if you fully stretch the boys arms then boy will not have any force in vertical direction to balance mg. It is not possible. So, answer will be infinity.
A simple way of thinking about it: Whenever you pull the boy, if you're to hold him in place you need to pull him up with the same force gravity is pulling him down. Since the force you can make in the boy is angled, that means you'll have to use a big enough force so that when you break it down to vertical and horizontal components the vertical one is at least as strong as his weight. The problem is that when you pull the boy the angle gets closer to the horizontal, and at each "step" you'll need to use a greater force in order to keep the vertical component big enough for the boy not to fall.
However,when the boy's arms are fully stretched, as you can see in the drawing, you will be pulling him horizontally, and so it is impossible for you to input a big enough force so that you generate a good vertical component, since no force you put in horizontally will generate a vertical result. In mathematical terms, since your force needs to get stronger and stronger as you pull the boy up, to achieve perfect horizontality you would need an infinite force. In a real application, you would never get a perfectly stretched arms, you would always end up in a close enough angle so that you consider horizontal.
The resultant force on the center of mass of the boy F R is given by in vectors F R = F + W , where ∣ W ∣ = 5 0 × 9 . 8 N is the weight of the boy. F R makes an angle θ with the vertical, where t a n θ = ∣ W ∣ ∣ F ∣ . For θ to be 9 0 ∘ , F must be ∞ .
when you pull the guy with the rope you apply a horizontal force. However the force which is actually bending his hands exists in the vertically downward direction. Though there is a vertical component of tension in the upward direction, as you pull him up, that component will vanish thereby making it impossible to take his hands to full horizontal.
Let the angle θ the angle between the head and the arm (for easy reason).
Draw all the force vectors...
From Newton's law, Σ F = 0 we get...
T sin θ = F
T cos θ = m g
Divide 2 equations we get...
tan θ = m g F .
For θ = 9 0 ∘ , tan θ = ∞ . So F = ∞ .~~~
Who did this to the boy, y u so mean. :< (jk he's naughty lol)