Can you survive from all magicians?
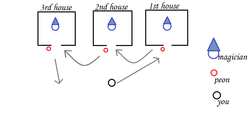There are three houses. There is a magician in each house. At the door of each house there is a peon who takes 2$ when-ever you enter or exit from the house. The magician in the house doubles your amount.
For example, if you have 5$, when you enter in first house, peon will take 2$ from you, Now you have 3$ left. The magician will double you amount to 6$, when you step out from the house the peon will take 2$ again then when you enter in 2nd house the peon will take 2$ again.... and so on.
Now you have to choose a specific amount that when you exit from the last house you have nothing in your hand (i.e, zero $).
{Type your answer like this...... 2 , 3.5 , 7.25 , ........}
The answer is 5.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
start everything backwards. let we have 0$ at the 3rd house by entering peon give us 2$.,magician divides it by 2, left us 1$. by exit peon give us 2$.total=3$. at 2nd house peon give us 2$ total=5. magician divides it by 2 and we are left 2.5 and by exit peon gives us 2 more. total=4.5. now at 1st house entering peon gives 2 so total =6.5 and magician divides it by 2 so we are left with 3.25. and at exit the peon gives us 2 more so total here are 5.25$. the ans is=5.25