Candy Corn Concentric Circles
In this diagram of four concentric circles, the combined area of the yellow regions is the same as the combined area of the orange and white regions.
z 1 , z 2 , z 3 , and z 4 are positive integers such that g cd ( z 1 , z 2 , z 3 , z 4 ) = 1 .
Must it be true that z 1 = z 2 = z 3 = z 4 ?
Diagram not necessarily drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
This is one of these moments, i think "Yeah this basically explains it in one sentence...or i do it with my 10 pages long explanation"...
Very good solution!
This is exactly what I did
That doesn't work. The greatest common divisor is not 1..You have two numbers the same (a is there twice) so these two numbers obviously have a common divisor a. Sets which do work are (1, 11, 5, 7) or (47, 41, 9, 23) which have no common divisors except 1.
Let z 1 = a , z 1 + z 2 + z 3 = b , and let z 1 + z 2 + z 3 + z 4 = c . Then, we have:
a 2 + c 2 − b 2 c 2 c 2 = b 2 − a 2 = 2 b 2 − 2 a 2 = 2 ( b − a ) ( b + a )
Given that a , b , and c are integers, we note the following:
- ( b − a ) ( b + a ) = 2 n 2 , where n is a positive integer.
- Since ( b − a ) ( b + a ) is even and b and a are integers, it follows that ( b − a ) and ( b + a ) must also be even.
- Then, it follows that ( b − a ) ( b + a ) = 8 m 2 , where m is a positive integer.
Now a bit of guess-and-check with different values of m to find a viable solution. With 8 m 2 = 7 2 , ( b − a ) = 4 , and ( b + a ) = 1 8 , we have:
a b c = 7 = 1 1 = 1 2
This gives ( z 1 , z 2 , z 3 , z 4 ) = ( 7 , 1 , 3 , 1 ) or ( 7 , 3 , 1 , 1 ) . Thus, it is not necessary that z 1 = z 2 = z 3 = z 4 .
How (b-a)(b+a)=2n^2 and how b-a and b+a are even
Log in to reply
From before, we have c 2 = 2 ( b − a ) ( b + a ) . Since c 2 is a perfect square, 2 ( b − a ) ( b + a ) must also be a perfect square. So ( b − a ) ( b + a ) must contain a factor of 2.
If you sum ( b − a ) + ( b + a ) , then you get 2 b which is even. Recall that
- even + odd = odd
- even + even = even
- odd + odd = even
Given that ( b − a ) ( b + a ) is even, both ( b − a ) and ( b + a ) must be even.
( z 1 , z 2 , z 3 , z 4 ) = ( 2 , 1 , 3 , 2 ) works, so, "No"
I am assuming that z 2 , z 3 , z 4 are distances between circumferences of circles, while r 1 is the radius of the smallest circle.
Yes, you are correct.
Andy Hayes updated the new version of my diagram, which does not indicate exactly the center point of circles.
Suppose that (a, a, a, a) is a solution and this quanterne satisfies gcd = 1. Since the gcd = a, then a = 1. But by congruence, any multiple of (1, 1, 1, 1) is also a solution. So both hypotheses cannot be true.
I am really confused that no one mentioned this idea in their solution... how come the gcd of 4 numbers is 1 if they are equal? except for the case where all of them are 1?
A counterexample tells the option.--- NO
Z1=3, Z2=1 Z3=5 Z4=3
Here note the following, If
Z1=Z4=k
And Z3+Z2=2k
all solution of (Z1,Z2,Z3,Z4,k) will satisfy the condition.
I just made a range of counterexamples, if z1=z4 and z1+z4=z2+z3 this will be no different from them all being equal. I, for example, used z1=1000, z2=1, z3=1999 and z4=1000, the only divisor of 1=z1 is 1 so the gcd must be 1 but it makes the same yellow, orange and white spaces as z1=z2=z3=z4=1000 which is just a scaled z1=z2=z3=z4=a for all a, so either this works or z1=z2=z3=z4 is wrong (and hence not true).
Start with the working solution given, and then increase z 2 and decrease z 3 such that z 2 + z 3 remains constant
We note that the areas of the white, yellow and orange regions depend only on z 1 , ( z 2 + z 3 ) , z 4 in fact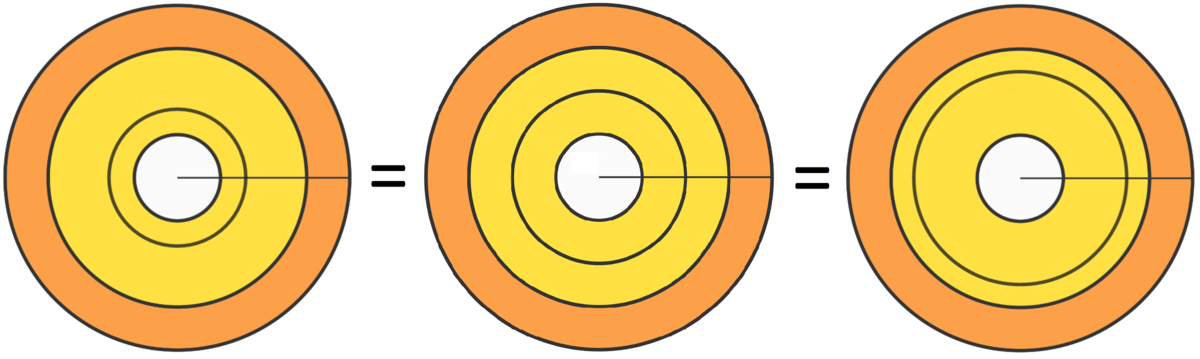 where the sign of equality indicates that the three regions are equivalent in the respective figures, therefore since the quaterne of the form
(
a
,
a
,
a
,
a
)
a
∈
N
work (except for the condition on the gcd), the quaterne of the form
(
a
,
a
−
k
,
a
+
k
,
a
)
a
∈
N
k
∈
Z
∣
k
∣
<
a
also work, now it is sufficient to choose k such that
g
c
d
(
z
1
,
z
2
,
z
3
,
z
4
)
=
1
i.e.
k
=
a
−
1
.
where the sign of equality indicates that the three regions are equivalent in the respective figures, therefore since the quaterne of the form
(
a
,
a
,
a
,
a
)
a
∈
N
work (except for the condition on the gcd), the quaterne of the form
(
a
,
a
−
k
,
a
+
k
,
a
)
a
∈
N
k
∈
Z
∣
k
∣
<
a
also work, now it is sufficient to choose k such that
g
c
d
(
z
1
,
z
2
,
z
3
,
z
4
)
=
1
i.e.
k
=
a
−
1
.