Candy Store!
 I went to the candy store last weekend and I bought a total of 10 packs of candy. I bought M&Ms for $1 per pack and Twizzlers for $0.50 per pack. I spent a total of $6. How many packs of M&Ms did I buy?
I went to the candy store last weekend and I bought a total of 10 packs of candy. I bought M&Ms for $1 per pack and Twizzlers for $0.50 per pack. I spent a total of $6. How many packs of M&Ms did I buy?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
81 solutions
nice way of solving it
The best way for solving this problem
& Thanks for giving such nice solution
My brain gave me an error after this ı did not even learnt this at school
Very easy way of solving
good question!!
I guess so. I solved it rationally though. No equation. Could be 4 or 2 also. It would be nice if it was more specific i guess. I put 4 first.
Log in to reply
It can't be 4 wut. 4 packs of M&M's --> 4$ spent, yet you bought 10 items in total which means you would have bought 6 twizzlers in addition, which would cost an extra 3$. Then you would have spent a total of 7$, not 6.
No to Ed Penny (5 M&M and 2 twizzler) because we are told ten items were purchased in total.
I am a math teacher. I'd go like this with my students for the resolution :
I don't like 0.5 (calculus/fraction) so I double the equation: 2x+y=12. With x+y=10, it gave me by substraction: x=2. I don't care about y.
You could have bought 5 m&m and two twizzler Lack of information can lead to multiple answers.
Write a system: x = Number of M&Ms, y = Number of Twizzlers
x + y = 1 0 and 1 . 0 0 x + 0 . 5 0 y = 6
Subtracting the equations: 0 . 5 y = 4 so y = 8 . It follows that there are 1 0 − 8 = 2 M&Ms
Just an general logic calculation that out of $6 if we take majority of total cost for more packs then we should need $0.5 packs more. Hence by applying basic operations we get (8x0.5)+(2x1)=6 Otherwise we can use equations as 1x+0.5y=6 and x+y=10 by solving we get x=2 and y=8 whereas x is no. of M&Ms pack and y is no.of Twizzlers
Log in to reply
But...how can u take that multiplication process Except that I all understood
Its says nothing about buying both types of candy
Log in to reply
I bought M&Ms for $1 per pack and Twizzlers for $0.50 per pack. Therefore meaning that at least one pack was bought of the Twizzlers. And because six dollars was spent, and ten packs of candy were bought, we can assume that he didn't get JUST M&Ms or JUST Twizzlers. As neither way would it add up to EXACTLY 10 bags.
True, but you couldn't satisfy both the conditions of the problem (10 packs bought, $6 spent) without buying a mixture of candy packs. For example, if only Twizzlers were bought, with 10 packs @ $0.50, you'd spend only $5; and for only M&Ms, you'd spend $10. You'd have to buy both to satisfy the conditions.
This solution is great. Congratulations.
really smart for such a young age
But they didn't asked for no. Of m&m
Can anyone explain this to me? I'm pretty weak in algebra.
Log in to reply
No algebra just use comman sense..... Twizzerls rate is 0. 50per if u buy 8 packs cost is 4. For remaning buy M&Ms......thats all
Basically becaus you need to have 10 pacers in total but t=0.5 and m=1 you have 6 in total so logically you know you need more of the value t so you have 8 packets of T and two of M
Even i used the method of simultaneous equations.
Great start, Harshal! However, the variable needs to represent the candy and use the same letter because you cannot simply subtract co-efficients and variables randomly..
For instance: let X represent each type of candy: x - M&M's and 2x = Twizzlers (there are twice as many packs of Twizzlers for each pack of M&M's) .
Then solve algebraically to find x, the M&M's. = )
why i assumed that m and ms is x and twizzlers is y ?
Log in to reply
Arbitrary value assignment. They could've used x for Twizzlers and y for M&Ms either way.
Need accurate solution
I am dumb as a rock…I was on the Dean's list in engineering college, I tutored a guy while taking the same calculus class, got A's in math, but I can't recall simple stuff like this. Maybe it would all come back real quick if I started doing it again…?
Or you can do
x+y=10
1x+.5y=6
Substitute
1m+.5(10-x)=6 then 1x+5-.5=6
.5x+5=6
x=2
What stops me from getting 3 M&Ms and 4 twizzlers or 1 M&Ms and 8 twizzlers, or 5 M&Ms and 2 twizzlers? The question doesn't clarify HOW you spent your money. The answer for this question is every possible combination of 1 and 0.5 that makes up to 6.
Log in to reply
It does clarify. It says you bought 10 packs of candy.... So 4 M&M and 4 Twizzlers would be wrong.
x + y = 10;
1x + 0.5y = 6;
==> 0.5y = 4
y = 4 /0.5 or y = 4/(1/2)
then y = 8;
subtracting now from the original 10..........
10 - 8 = 2;
so there were two packs of M&Ms bought.
but I didn't really use the formula. I counted on my head. simple calculation does it. no need for formulas and equations.
you could solve it rather in an easy way. well done.
just where in the Philippines were living christine dino?
Hmm... the answer could be 1 though😫
How did you solved this mentally? Maybe it took you long time to do it.
THE ANSWER TOOK SOME THOUGHT BUT I FINALLY GOT THE CORRECT ANSWER ! (3)
This is a basic question all you know is that: The payment for the amount of Twizzlers is a whole number The no. of packets for both sweets are number bonds of ten There no. of both packets are even numbers So if you got 1 M&M packet then you'd get 9 Twizzlers. That doesn't obey our even number rule. So if you got 2 M&M packets then you'd get 8 Twizzlers. This seems to work with our rules. You then do to check 5*8=40 add a zero for canceling=$4.00+$2 (from the M&Ms)=$6
It's strange solution.
Make a system :
x = Number of M&M
y = Number of Twizzlers
Total of candies : x + y = 1 0
Prize of candies : 1 x + 0 . 5 y = 1 0
Change the equations to function with x variable.
f ( x ) = y = 1 0 − x
f ( x ) = y = 0 . 5 6 − x
Plot these functions and see it.
P.S : It's strange, after all. Hehe.
Nice solution Indra!
innovative thinking!!
Brute force
(python)
total_packs = 10
mms_rate = 1
twizz_rate = 0.50
for mms_count in range(7): # worst case is 6 mms pack
if mms_count*mms_rate + (total_packs - mms_count)*twizz_rate == 6:
print mms_count
>>2
☆ Original ☆ I will present this method to my students.
Let all 10 packs of candy be M&Ms. So the total cost is $10. $10-$6=$4 (Find the price difference between if he had bought all M&Ms and the real number of packets of M&Ms he bought.) Since $4 is the difference, $4/$0.5=8 (to find the number of Twizzlers he actually bought.) Then 10-8=2 He bought 2 M&Ms!! Note: the other way can be done too. (assume all 10packs of candy are Twizzlers)
It makes no sense....you can't buy ten packs of anything listed for 6 dollars
I used exactly the same logic. The beauty is that one hand it is free of x and y and on other hand it is not hit and trial or speculation but pure logic and mathematics.
I just used logic. 6 packs at $1 is $6. 5 packs is $5 with 2 more at $.50 for total of 7 packs. 4 packs is $4 and 4 more at $.50 for total of 8. 3 packs is $3 and 6 more at $.50 for total of 9. 2 packs is $2 and 8 more at $.50 for total of 10.
if i buy 1 packet M&Ms,then i have to buy 9 packet Twizzlers,so the cost will be=5.50$
if i buy 2 packet M&Ms ,then i have to buy 8 packet Twizzlers,so the cost will be=6 $ ...................[the answer]
it,s easy all i have to do is 8 twizzlers =$.4.00+2m&m(2,00$)=$6.00 and 10 candys
Make a T-chart; no equations needed. Left side is # of packages, right side is $.
Make a random combination of Twizzlers and M&Ms until you reach $6 worth. NOTE: You must have an even # of Twizzlers.
Count your total packages of candy. If it's not 10, you need to either add or subtract packages.
TOO MANY packages? Swap out 2 Twizzlers for 1 M&M. TOO FEW packages? Swap out 1 M&M for 2 Twizzlers.
Do this until you reach 10 total packages.
Let X be the number of M&M's and the rest of the ten packs be the Twizzlers, or 10-x...
multiply each to their corresponding price and equate the total to 6
(x)(1)+(10-x)(0.50)=6
(x)+(5-0.50x)=6
x+5-0.50x=6
x-0.50x=1
2(0.50x=1)
x=2
You can eaither use a formula, but, if you're like me, on vacation with no paper, just use your fingers and try to raise them all up, using intervals of 1
M= no of M&M's, T=No of Twizzlers
M + T = 10
M + 0.5T = 6
From the second equation you can rearrange so T = 12 - 2M
Replace in the second equation
M + 12 - 2M = 10
-M = -2
M=2
My explanation would be logical and not hit and trial but without using x and y.
Had I bought 10 Ms (abbreviation) it would have cost me $10 but it cost me $4 less than that. Now if I buy 1 T (abbreviation) instead I would spend 50 cents less than 10 or we can say if there are 2 Ts it will be $1 less than $10. In order to reduce the price by a total of $4 I need to buy 8 Ts.
Going the other way round if I buy 10 Ts I would spend $5. Purchasing one M instead would raise the cost by 50 cents. In order to raise the cost by $1 (up to 6) I need to buy 2 Ms. Coming to the same conclusion as the first one.
P.S. I am thinking that maybe we can solve all the simultaneous equations by taking arbitrary values for one equation and then rationally working out to change them so that they also satisfy the second equation.
{ a + b = 1 0 a + 0 . 5 b = 6 = 0 . 5 b = 4 ⟹ b = 8
a + b = 1 0 = a + 8 ⟹ a = 2
I found out by using the system of estimation taking she spent 4 $ of twisllers and 2 dollars on m&m. Keeping in mind 1$ = 2 twizllers
Matrix: [1 1 10; 1 .5 6] Row Reduced Echelon Form: [1 0 2; 0 1 8]
You bought 2 packs of M&Ms and 8 packs of Twizzlers.
One method is:
Let M&Ms be m
Let Twizzlers be t
6m + 0t = $6 + $0 = $6 ............6 + 0 = 6
5m + 2t = $5 + $1 = $6 ............5 + 2 = 7
4m + 4t = $4 + $2 = $6 ............4 + 4 = 8
3m + 6t = $3 + $3 = $6 ............3 + 6 = 9
2m + 8t = $2 + $4 = $6 ............ 2 + 8 = 10 * This is the only solution which gives a total of * 10 packets .
1m + 10t = $1 + $5 = $6 ..........1 + 10 = 11
0m + 12t = $0 + $6 = $6 ..........0 + 12 = 12
Therefore, 2 is the number of packets of m ( M&Ms ).
m = M & M chocolates
t = Twizzlers
m + t = 10 .....(1)
1m + 0.5t = 6 .....(2)
by elimination or substitution;
m = 2 packs
I went with maximums and minimums. Since 9 twizzlers leave .45 then I went with 8.
You can write this problem with m being the M&Ms and t being the Twizzlers. We know that that total amount of candy is ten packs, so we can write this as: 1m + 1t = 10 (m is also 1m, as with t) We also know that the total amount of money is six dollars. We can write this as $1 per M&M, or 1m, plus $0.50 per Twizzler, or .5t, as: 1m + .5t = 6 We can change 1m +.5t to 1m + 1t, or 10 as: 1m + .5t = 10, but that would be wrong, because 1m + 1t = 10. Remember that whatever you do to one side, you have to do to the other. We can do the equation as: 1m + .5t = 10 - .5t, because if you add .5t to both sides, you get 1m + 1t = 10, which is the same as the first equation. We now know how to get the total of six dollars into the equation as: 6 (or 1m +.5t) = 10 - .5t We can find t this way. 6 = 10 - 4, so .5t must equal 4. Divide both sides by .5, and you get t of being 8. From the first equation, we can now substitute t as 8, now: 1m + 8 = 10, subtract both sides by 8, and you get: 1m (or m) = (10 - 8, or 2) m, or the packs of M&Ms you bought, is two packs.
I probably did too much.
a = $1 (M&M). b = $0.5 (Twizzlers). n = # of packets
For this method these two equations must be true. na + nb = 6 n + n = 10
Using different quantities for n and you'll be left with the only possible option. 8a + 2b = $10 6a + 4b = $8 4a + 6b = $7 2a + 8b = $6
2 M&M + 8 Twizzlers.
Anyone considering the sale of chocolate at the candy store
The problem gave all the clues.
Given:
they bought 10 packs of candy.
M&m's cost a dollar
Twislers .50
I didn't get I right their first time. Cause I thought they only bought 1, since I figured they bought more Twislers than M&m. What clued me in was the section of the story where they bought more than one pack of M&m's and the total was $6.
After that ah ha moment I counted in how many Twislers they purchased thst would equal 6 dollars and the removed 2 dollars worth
x+y=10
1x+.5y=6
Substitute
1m+.5(10-x)=6 then 1x+5-.5=6
.5x+5=6
x=2
Trail and error, 10 packs in total for $6, 8 Twizzlers equal $4, So theres $2 left for 2 packs of M&Ms
x+y=10 & x+.50y=6 Two equation two unknown. On solving x=2& y=8
If We say M&Ms = 10-x Twizzlers = x
after this system we write a formula
(10-x)1$ + 0,50$x = 6 $ => 10-x+0,50x = 6 and from this equation x=2
so that I bought 2 packs of Twizzlers but We are demanded M&Ms is 10-x = 10-2 =8
m&m = x; twizzlers = y x+y1/2=6 But x + y = 10 The numbers can only be even, because, since y is $0,50, the result can't be exactly $6,00 if there is an odd number for $0,50. So, X and Y can be: (2,8), (4,6), (6,4) or (8,2). Then, you just need to replace: 2+8 . 1/2=6 2+4=6 So, X=2. You don't even need to see if the other possibilities are right.
Think about it there 10 packs and only 6 dollars Try using trial and error like this: 1 mm. And the amount of twinkles Keep doing this until you reach the perfect amount
2 packs of m&ms plus 8 packs of twirlers is $6
Twiz=8x0.50=4
MM=1.00x2=2
4+2=6
Let's think that X is for M&Ms and Y for Twizzlers (i) for the 1st statement, it will be the formula "I bought M&Ms for $1 per pack and Twizzlers for $0.50 per pack.", so it will be : 1x + 1y = 10 (ii) for the 2nd statement who was the action "I spent a total of $6." Because we don't know how many 'I' bought M&Ms, so we need to search it, in Junior and High School we all ever learned about this in Math subject, and maybe also in Tech Logic, so it will be : 1x + 0.50y = 6
It called subsitution and elimination, So now, we want to eliminate the 'X' first, and because the 'X' has already same, so we can just elimanted it now with minus the 1st statement with 2nd statement. The result is : 0.50y = 4 | y = 4/0.50 | y = 4 * 2 = 8 It means, that 'I' bought 8 packs of Twizzlers.
Now, we need to substitute them : You can choose, to using 1st statement or 2nd statement, it just the same.
With 1st statement : 1x + 1y = 10 1x + 1(8) = 10 1x + 8 = 10 1x = 10 - 8 x = 2
With 2nd statement : 1x + 0.50 y = 6 1x + 0.50(8) = 6 1x + 4 = 6 1x = 6 - 4 x = 2
Means that 'I' bought 2 packs of M&Ms.
x + y = 10 (number of items)
x = 10 - y [1]
1 * x + 0.5 * y = 6 (price)
x + (y/2) = 6 [2]
[1] in [2]
(10 - y) + (y/2) = 6
(20 - 2y + y) / 2 = 6
20 - 2y + y = 6 * 2
20 - y = 12
-y = 12 - 20
-y = -8
[by -1]
y = 8
A little educated mental guess-and-check:
It is possible to have purchased one to nine packs of M&Ms (since you bought both kinds of candy). Since the total price is a whole number of dollars ($6) you must have purchased an even number of Twizzlers, leaving an even number of packs of M&Ms. Now, the possibilities are 2, 4, 6, and 8 packs of M&Ms. 6 or 8 packs of M&Ms would exhaust all $6 spent, so you must have bought 2 or 4.
2 M&Ms and 8 Twizzlers cost $6, while 4 M&Ms and 6 Twizzlers cost $7.
So, you bought 2 packs of M&Ms.
Suppose that x is many of M&Mrs candy and y is many of Twizzlers so we have two equation, x+y=10 and x+0,5y=6. Then, substitute equation one to equation 2 so we get the value of x is 2. So, the answer is 2.
suppose that M & M's and Twizzlers numbered x and y we get x + y = 10 the price of M & M's are 1 and Twizzlers is 0.5 we get 1 (x) + 0.5 (y) = 6 elimination y! x + 0.5y = 6 then 2x + y = 12 we have 2x + y = 12 and x + y = 10 if eliminated obtained x = 2
If X is the Number of M&Ms and Y be the number of Twizzlers then,
X+Y=10
and
X + 0.5Y=6
Upon solving
X=2 ==>M&Ms
Y=8
The person spent 6 dollars so there has to be less than 6 M&M packs. The number of packs of Twizzlers has to be an even number since 6 is a whole number. so the only 2 combinations possible are (m being M&Ms and t being Twizzlers): 2m + 8t, and 4m + 6t. 4(1) + 6(.5) = 7 therefore 2m + 8t is correct. So the person bought 2 packs of M&Ms.
This Ques can be solved by using Allegation method. Let's first assume that he only bought 10packs of MM. Then his total expenditure is $10. Now assume, that he only bought 10 packs of LWZ. Then his total expenditure would be $05.
But in reality he only buy a mixture of MM and LWZ of 10 packs in $06.
Now the the ratio of MM and LWZ would be (06-05) : (10-06) = 1:4...which in turen would be 2 : 8 (8+2=10)
Twizzlers(T)--> $0.5(cost of per pack of T)x8(number of packs of T)=$4
M&M(MM)---> $1(cost of per pack of MM)x2(number of packs of MM)=$2
Total cost=$6
Total Number of packs of candy=10
let us take m&m packs be x & twizzlers to be y. so x+y=10 and 1x+0.5y=6 by solving this we get x-1x+y-0.5y= 10-6 0+0.5y=4 so y=8 10-y=x 10-8=x x=2
a+(10-a)/2=6 ..... a+10=12 ........ a=2
Mathematics offers many strategies. Here is one:
Let's use x to represent the $1 M&M's and 2x represents the Twizzlers, because we can get 2 Twizzlers for each bag of M&M's. [2Twizzlers ($0.50) for every 1M&M ($1)].
We know that if we add our M&M's (x) and our Twizzlers (2x) it will equal $6 and will indicate how many $1 items were in teh $6.
So...
x + 2x = $6 (add like terms 1x + 2x) 3x = 6 (divide by 3 to isolate the variable; remember what you do on one side of the equation symbol you must do on the other) x = 2
So...
$6 - $2 = $4
Therefore, two packages of M&M's ($2) was purchases and $4 (eight packages) of Twizzlers were purchased.
You could also draw a diagram using 6 rectangles to indicate the each of the $'s in the total purchase; $6. Then you could work by trial and error. Start with the first rectangle...that would be 1 bag of M&M's which is $1. That would leave $5 for Twizzlers....however, that would be 10 Twizzlers and 1 bag of M&M's, which is 11 total packages...one too many. Next, Start with the first 2 rectangles...that would be $2 of M&M's, which leaves $4 for Twizzlers...or eight packs of those. So 2 packages of M&M's for $2 and 8 packages of Twizzlers for $4 or total cost $6. :)
Let number of M&Ms be x, so number of twizzlers will be 10-x.
By writing down the equation 1x + 0.5(10-x) = 6 , you will get x as 2.
I I I 0.5 0.5 0.5 0.5 0.5 0.5 AND 0.5 DOLLAR IS LEFT SIMPLE :)
2 ways 1 is simple logical observation 10nos , 6$ ...... 8 nos* 0.5 =4$ and 2nos 1=2$ second is equation X(nos) +Y(nos)=10 and X amount +Y*amount=6 solve X+Y=10 , X+0.5Y=6
- 1x1=1 _ _ _ _ 9 x .5 = 4.5 _ _ _ _ _ 4.5+1=5.5
- 2x1=2 _ _ _ _ 8 x .5 = 4 _ _ _ _ _ 4+2=6
A system of equations would be fine, but this case is so simple that you can do some mental calculations. The number of Twi must be even, of course. Eleminating 10 ,'cause there's also MnM, we start at 8 and fortunately it's the answer
The easiest way is guest: Number of Twizzlers must bi even 2,4,6,8 Just test and find the result
i just used common sense
I counted on my fingers.
Each finger represents a dollar which is two Twizzlers or one M&Ms. Now I need to find which combination of six fingers gives me ten packs of candy.
Counting by twos a finger a time (that would be your Twizzlers), I continued until I got to the point (4 fingers) where my Twizzlers number (8) plus the balance of fingers equaled 10 (2, which would be your M&Ms). Piece o' cake (arf arf, humor).
x=MMs, y=Twizzlers
Using the information given we know the following: x + y = 10 ; x + .5y = 6
Add the 2 equations together and you get:
x + y =10
x + .5y = 6
2x + 1.5y =16
We need to isolate one variable so using : x + y =10 we know that x = 10 - y
Now we rewrite the equation in terms of y:
2(10-y) + 1.5y =16
20 - 2y + 1.5y = 16
-0.5y = -4
y = 8
We know from previous equation that x = 10 -y, so we can now solve for x:
x = 10 - y
x =10 - 8
x = 2
You bought 2 packs of MMs.
x + y = 10 x + 0.50y = 6
y = 8, x = 2
Total number of M&Ms and Twizzlers = 10 Say x = number of M&Ms, then number of Tizzlers = 10 - x $1 (x) + $0.5 (10 - x) = $6 $x + $5 - $0.5x = $6 $0.5x = $1 --> x = 2 packs (of M&Ms)
Quantities=10 packs=Q
M&Ms= $1=x
Twizzlers=$0.50=y
Total price=$6=P
The formula that express the price(P) and the quantities of packs bougth of M&Ms(a) and Twizzlers(b) is:
P = a x + b y P = 1 a + 0 . 5 b P = a + 2 b
The quantities are express by this formula:
Q = a + b 1 0 = a + b
We want the value of a:
b = 1 0 − a P = a + 2 1 0 − a 6 = a + 2 1 0 − a a = 2
Sea que (1)... x+y=10 (2).... x+1/2y=6
Realizando operaciones 1/2y=4 entonces y=8 Por sustitución 10-8=2
I bought total of 10 packs. Possible combination is 2 ($1) + 8 ($0.50) = 2 + 4 = $6 (which I actually spent).
Where 2 (are of M&M) and 8 (are of Twizzlers).
the 10 packs candies consists of some M&Ms and Some Twizzlers. I will make it looks like : 10 = x + y then, 10 - y = x
x + 0.5y = 6 then, convert the x into : 10 - y + 0.5y = 6 || -0,5 y = -4 OR y = 8 -> number of Twizzlers are 8
Now, back to the first when x + y = 10 then, x+ 8 = 10 x = 2 -> total number of M&Ms are 2
Let x be the no. of M&Ms and y be the no. of Twizzlers, So, we know that x+y=10 (since he bought 10 candies on the whole) also, we know that 1.00x+0.5y=6 (he spent six dollars) on solving simultaneously, we get 0.5y=8. so y=4. therefore, there are 10-8=2 M&Ms
Let,
$0.5*8 = 4,
$1*2 = 2
Here the price of M & Ms per pack is $1 so I had to buy not more than 2 packs.
Let, the no. of M&Ms packs bought = x So, the no. of Twizzlers packs bought = (10-x) As, each M&Ms pack costs $1, x packs cost = (x* $1) = $ x As, each Twizzlers pack costs $0.50, (10-x) packs cost = (10-x)* $0.50 =$(5-0.50x)
According to the question, the total cost incurred = $6
So, $ x +$(5-0.50x) = $6 or, $ x - $ 0.50x = $6 - $5 or, $ 0.50x = $1 Thus, x = 2 So, the no. of M&Ms packs bought = 2
Let be all the packets of M&Ms i.e. 1$ x 10= 10$ 10$ - 6$ = 4..i.e number of packets of twizzlers And the rest i.e. 2 packets are of M&Ms
M&ms got 2 packs of candy... Just elementry prob.
Create a system of equations - (x is Twizzlers, y is M&Ms)
. 5 x + y = 6 (This one is comparing individual prices with total cost of entire transaction)
x + y = 1 0 (This one is total packs of candy bought with individual candy packs)
We need to isolate y because that is our M&M variable.
x = 1 0 − y
We then substitute it in.
. 5 ( 1 0 − y ) + y = 6
5 − . 5 y + y = 6
. 5 y = 1
y = 2
This is how we know he bought 2 packs of M&Ms
Um I just do it in my head. No y ' s no x's. I think what number the prices break down to equal the total.
M&M+Twizzlers=10 M&M+0.5*Twizzlers=6 => M&M=2 (Twizzlers=8)
say, M&Ms bought=x packs twizzlers bought=(10-x) packs
now, x 1+(10-x) 0.5=6 or. x+10*0.5-0.5x=6 or, x+5-0.5x=6 or, 0.5x=6-5 or, 0.5x=1 or, x=1/0.5=2 (ans)
Try to do trial&error method
x+y=10 -------(1) x+0.5y=6-------(2) after solving these equations answer is 2
X= M&ms Y= Twizzlers
x+y=10 x+y/2=6
y=10-x y=12-2x
10-x=12-2x x=2 = M&ms
Just work out factors . 1,9 8,2 6,4 5,5 7,3 . If you have something .50 you know it cant work . I just used trial and error and eventually 8x0.50 = 4 and then youd add 2 to make up to 6 so 2 x $1 m and ms . Others wouldnt work such as 9x0.50 = 4.50 meaning you need 1.50 to make it up which isnt possible with $1 bags
Well,the average of the prices per pack is 6/10=0.6.So we can know that packs of M&Ms over packs of Twizzlers is (0.6-0.5)/(1-0.6)=1:4,so packs of M&Ms take up one fifth of 10,the total. 10*1/5=2
Very simple. Call "x" is M&M packs and "y" is Twizzlers packs. There are total 10 packs so x+y=10 (1). Beside that, the total money is $6. An M&M pack costs $1 so "x" packs cost 1 times x; the Twizzlers cost $0.5 so "y" packs cost 0.5 times y. Hence, we have x + 0.5y = 6 (2). From (1) and (2) we have the equations and you can solve it easily ^^ (this quiz is so easy, in my country we've learned it since we were in grade 6)
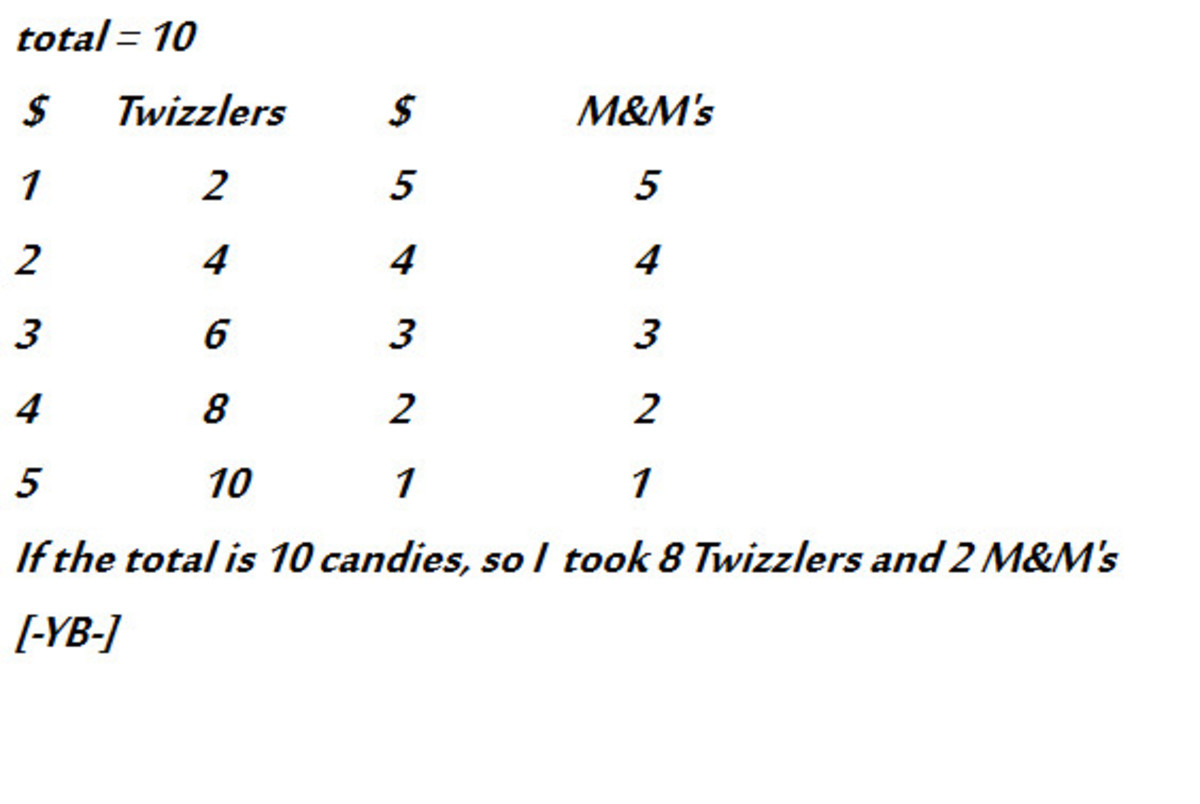
Write a system of equations where x is the number of M&Ms and y represents the number of Twizzlers.
{ x + y = 1 0 x + 0 . 5 y = 6
Note that y − 0 . 5 y = 1 0 − 6 0 . 5 y = 4 y = 8
And x + y = 1 0 x + 8 = 1 0 x = 2
So, you bought 2 packs of M&Ms