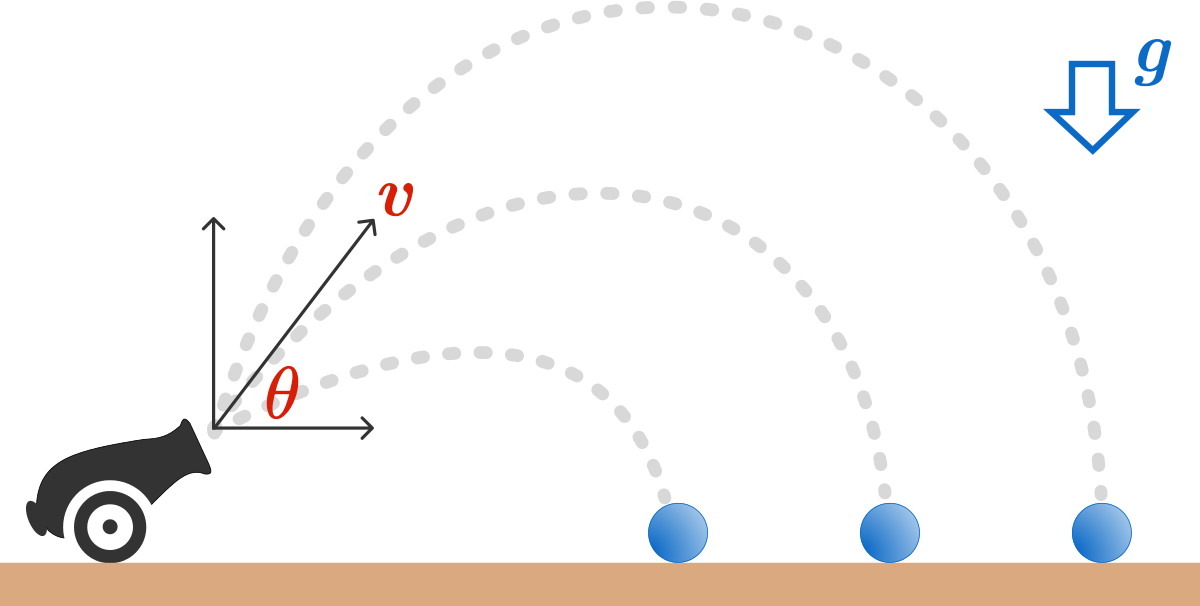
Cannon Shot Variance

Let us call velocity in the $x$ -axis as $v_x$ and velocity in the $y$ -axis as $v_y$ .

Thus:

$\large \displaystyle v_x = v \cos (\theta)$

$\large \displaystyle v_y = v \sin (\theta)$

Being $t$ the time for the ball to reach its highest point from ground:

$\large \displaystyle 0 = v_y - 10t$

$\color{#20A900} \boxed{ \large \displaystyle t = \frac{v \sin(\theta)}{10} }$

The total time that the ball will be in air is $2t$ , and then:

$\large \displaystyle D = v_x \cdot 2t$

$\color{#20A900} \boxed{ \large \displaystyle D = \frac{ v^2 \sin(2 \theta)}{10} }$

So, the variance will be:

$\large \displaystyle \sigma^2 [D] = E[D^2] - E^2[D]$

$\large \displaystyle \sigma^2 [D] = \left [ \frac{1}{500} \cdot \frac{1}{\frac{\pi}{2}} \int_0^{\frac{\pi}{2}} \int_0^{500} \frac{v^4 \sin^2 (2 \theta) }{100} dv d \theta \right ] - \left [ \frac{1}{500} \cdot \frac{1}{\frac{\pi}{2}} \int_0^{\frac{\pi}{2}} \int_0^{500} \frac{v^2 \sin (2 \theta) }{10} dv d \theta \right ] ^2$

$\large \displaystyle \sigma^2 [D] = \left [ \frac{1}{25000 \pi} \frac15 v^5 \Bigg | _0^{500} \cdot \int_0^{\frac{\pi}{2}} \left ( \frac{1 - \cos(4 \theta)}{2} \right ) d \theta \right ] - \left [ \frac{1}{2500 \pi} \frac13 v^3 \Bigg | _0^{500} \cdot \frac{\cos (2 \theta)}{2} \Bigg | _{\frac{\pi}{2}}^{0} \right ] ^2$

$\large \displaystyle \sigma^2 [D] = \left [ \frac{1}{25000 \pi} \frac15 500^5 \cdot \left(\frac{\pi}{4} - \frac{\sin (4 \theta)}{8} \Bigg | _{0}^{\frac{\pi}{2}} \right ) \right ] - \left[ \frac{1}{2500 \pi} \frac{500^3}{3} \right ] ^2$

$\large \displaystyle \sigma^2 [D] = \frac{500^5}{500000} - \frac{500^6}{56250000 \pi^2}$

$\color{#3D99F6} \boxed{ \large \displaystyle \sigma^2 [D] \approx 34355226.766 }$