Can't See The Forest From The Trees
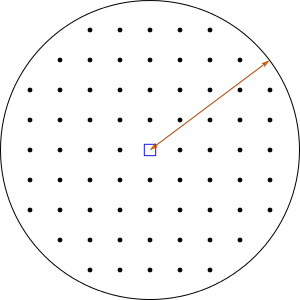
There is a circular fence of radius R = 2 5 m that encloses an orchard. The trees in the orchard are laid out on the vertices of a square lattice of edge 5 meters. The trees are circular with equal radius, and do not grow where there is a fence. At the very center, instead of a tree, there stands a man.
What is the minimum radius for the trees (in meters) such that the man cannot see the fence?
Hint : think at Minkowski's theorem.
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
When you say 1 is the correct answer you miss that (20,15) will block some vision between (5,5) and (15,10) in method 2. So the correct answer is 0.98.
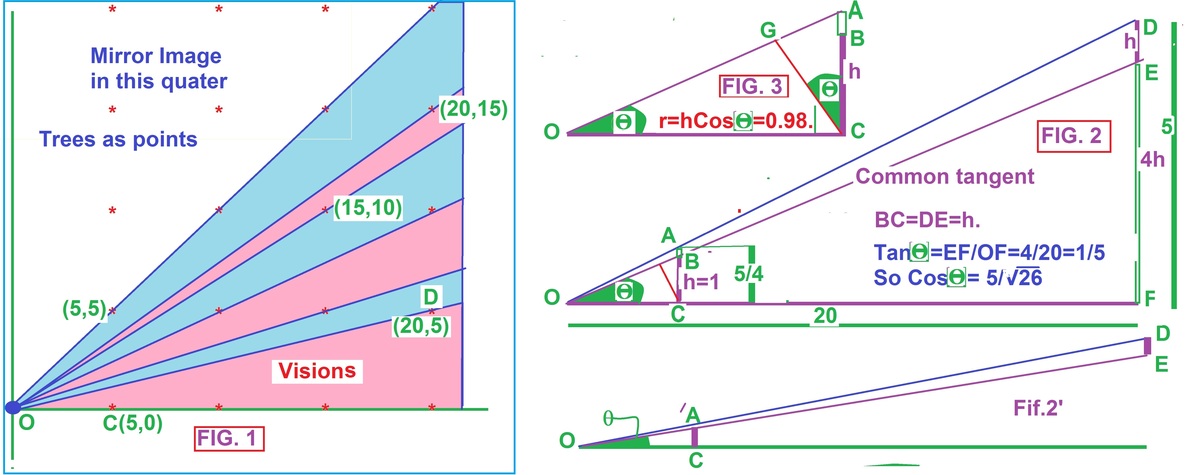
I think the given answer is no correct. My answer is correct. My solution:-
The square lattice has 8 fold symmetry, so we shall look only at 45 degrees of the lattice.
Fig. 1 shows assumes trees as points and zones between critical trees are shown.
It is obvious that Top blue zone between (5,5) and (20,15), and Bottom pink zone between (5,0) and (20,5) needs widest blocking.
But Top zone is at a bigger slope, trees near (0,0) will block more than trees near (0,0) from the Bottom zone. So they need a shorter
radius than the the Bottom zone. Hence only bottom zone is critical.
In order to block full sight, there should be no gap between tangents to (5,0) and (20,5). Implies they have a common tangent.
Fig. 2 Shows this common tangent OE between lines OD and OF.
OD, OE, OF is intersected by up vertical from C at A, B, C.
OD, OE, OF is intersected by down vertical from D at D, E, F.
ABC and DEF form various similar right triangles with common angles at O. Hence the following ratios.
BC/EF=OC/OF=1/4, but OC=5, OF=20, and DF=5, also BC=DE= say h.
Therefore EF=4h , but DE+EF=h+4h=5h, also DE+EF=DF=5, implies h=1.
T
a
n
θ
=EF/OF=4/20, implies
C
o
s
θ
=
2
6
2
5
.
In Fig. 3, right triangles OBC and CBG have
θ
same.
S
o
r
=
h
∗
C
o
s
θ
=
2
6
2
5
=
0
.
9
8
.
Try to check the case you eliminated (the one between (5,5) and (15,10)). Note that a tree cannot grow were the fence is, this means that (20,15) is not at tree. In the previous solution it is case 1. There are 2 critical zones which have to be analysed: the bottom one (which you already done) and the top one (between the critical trees (5,5) and (15,10)).
Log in to reply
Please note that the radius i s 25, so there is a tree at (20,15).
Log in to reply
I am verry sorry for the confusion created. I should have explicitly mentioned this in the problem. I will modify it now.
Here are two methods to solve this.
Method 1
Let's call the radius of the trees r . Through the center O draw any line which intersects the boundary of the orchard in points M and N . Then draw the tangents to the circle in these two points. Now construct two lines A D and B C parallel to M N at a distance r . The rectangle
A
B
C
D
has the area
A
=
2
r
2
R
=
4
r
R
. By Minkowski's theorem if
A
>
4
d
(
L
)
then the area
A
contains at least two lattice points
P
and
Q
which are symmetric about
O
, therefore the line
M
N
intersects these trees. The determinant of the lattice
d
(
L
)
is the n-dimensional volume of the fundamental parallelepiped, which in our case is
d
(
L
)
=
d
2
=
2
5
m
2
. So
4
r
2
5
m
>
4
⋅
2
5
m
2
which gives
r
>
1
m
.
The rectangle
A
B
C
D
has the area
A
=
2
r
2
R
=
4
r
R
. By Minkowski's theorem if
A
>
4
d
(
L
)
then the area
A
contains at least two lattice points
P
and
Q
which are symmetric about
O
, therefore the line
M
N
intersects these trees. The determinant of the lattice
d
(
L
)
is the n-dimensional volume of the fundamental parallelepiped, which in our case is
d
(
L
)
=
d
2
=
2
5
m
2
. So
4
r
2
5
m
>
4
⋅
2
5
m
2
which gives
r
>
1
m
.
Method 2
The same result is obtained by drawing a radius tangent to the trees, then calculating the radius of the trees. Because of the symmetry of the orchard there are two cases to be analysed.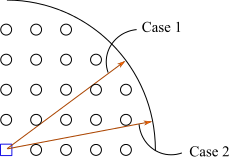 In the first case the two trees that will come in discusion have the coordinates
M
1
(
5
,
5
)
and
M
2
(
1
5
,
1
0
)
. Using the formula for the distance between a point and a line
r
=
1
+
m
2
∣
y
0
−
m
x
0
−
n
∣
and considering that the line goes through the origin:
1
+
m
2
∣
5
−
5
m
−
0
∣
=
1
+
m
2
∣
1
0
−
1
5
m
−
0
∣
⇒
m
1
=
2
1
,
m
2
=
4
3
The first value has the trees on the same side and it's not good. The second value is the good one. Going back to the distance formula with this slope gives:
r
=
1
+
(
4
3
)
2
∣
∣
5
−
5
4
3
∣
∣
=
1
6
2
5
5
4
1
=
1
If
r
=
1
then the line is tangent to the trees. So
r
>
1
.
In the first case the two trees that will come in discusion have the coordinates
M
1
(
5
,
5
)
and
M
2
(
1
5
,
1
0
)
. Using the formula for the distance between a point and a line
r
=
1
+
m
2
∣
y
0
−
m
x
0
−
n
∣
and considering that the line goes through the origin:
1
+
m
2
∣
5
−
5
m
−
0
∣
=
1
+
m
2
∣
1
0
−
1
5
m
−
0
∣
⇒
m
1
=
2
1
,
m
2
=
4
3
The first value has the trees on the same side and it's not good. The second value is the good one. Going back to the distance formula with this slope gives:
r
=
1
+
(
4
3
)
2
∣
∣
5
−
5
4
3
∣
∣
=
1
6
2
5
5
4
1
=
1
If
r
=
1
then the line is tangent to the trees. So
r
>
1
.
For the second case when M 3 ( 5 , 0 ) and M 4 ( 2 0 , 5 ) the same calculations give m 3 = 3 1 and m 4 = 5 1 . Going back with m 4 gives the radius r = 2 6 2 5 ≈ 0 . 9 8 . So it is not worthy looking to the fence like in case 2. So the final value is r > 1 m .