Cantor Sequence

Computer Science Level 3

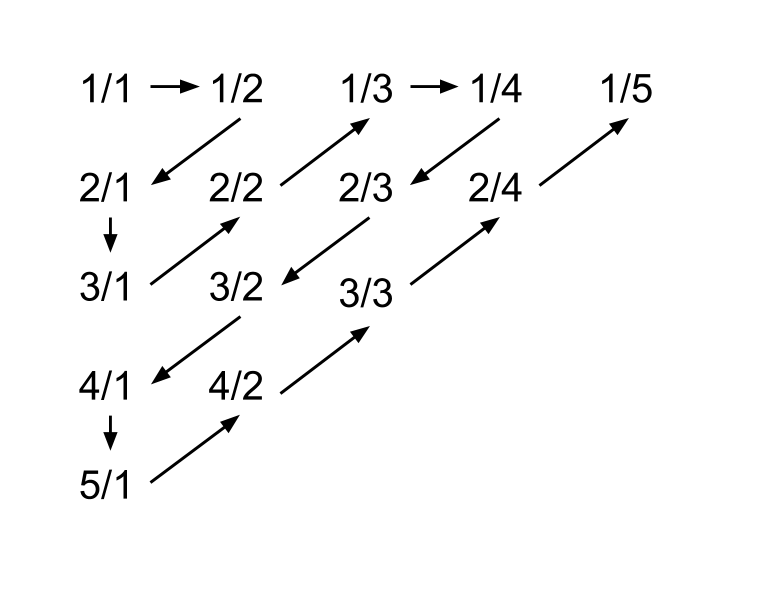
Consider the sequence $\{ 1/1, 1/2, 2/1, 3/1, 2/2, 1/3, \ldots\}$ as shown above.

What is the $3974^\text{th}$ term?

\frac{30}{60}

\frac{30}{61}

\frac{31}{58}

\frac{31}{59}

\frac{32}{58}

\frac{33}{57}

2 solutions

Rushikesh Jogdand
Jun 21, 2016

def Next(_List):
    i=_List[0]
    j=_List[1]
    bl=_List[2]
        # i : numerator
        # j : denominator
        # bl : whether to head Bottom Left or not
    if bl:
        if j==1:
            I=i+1
            J=1
            BL=False
        else:
            BL=True
            I=i+1
            J=j-1
    else:
        if i==1:
            I=1
            J=j+1
            BL=True
        else:
            BL=False
            I=i-1
            J=j+1
    return [I,J,BL]
term=[2,2,False]
count=5
while count!=3974:
        count+=1
        term=Next(term)
print(term[:2])

Chew-Seong Cheong
Jun 20, 2016

Consider the slanting diagonals as rows. We note that the last term of row 1 is 1st term, row 2 is 3rd term, row 3 is 6th term, row 4 is 10th term and so on. This means that the last term of $n$ th row is the $T_n$ th term of the sequence, where $T_n = \dfrac {n(n+1)}2$ is the triangular number.

By putting $\dfrac {n(n+1)}2 = 3974$ $\implies n \approx \lfloor \sqrt{2 \cdot 3974} \rfloor = 89$ . We note that $T_{88} = \dfrac {88\cdot 89}2 = 3916$ and $T_{89} = \dfrac {89\cdot 90}2 = 4005$ . Therefore, the 3974th term is in the 89th row.

We note that for odd $n$ , the first term (starting from bottom) of $n$ th row $a_{n, 1} = \dfrac n1$ , the second term $a_{n, 2} = \dfrac {n-1}2$ , the third term $a_{n, 3} = \dfrac {n-2}3$ , ... $\implies a_{n, k} = \dfrac {n-(k-1)}k$ .

Now, we have $n=89$ and $k = 3974-3916 = 58$ , $\implies a_{89, 58} = \dfrac {89-57}{58} = \boxed{\dfrac{32}{58}}$ .

Cantor Sequence

2 solutions

0 pending reports