Capacitor Exercise (part 2)
A non-relativistic charged particle flies through the electric field of a cylindrical capacitor and gets into a uniform transverse magnetic field with induction
as shown in figure. In the capacitor the particle moves along the arc of a circle, in the magnetic field, along a semicircle of radius
. The potential applied to the capacitor is equal to
, the radii of the electrodes are equal to
and
with
.
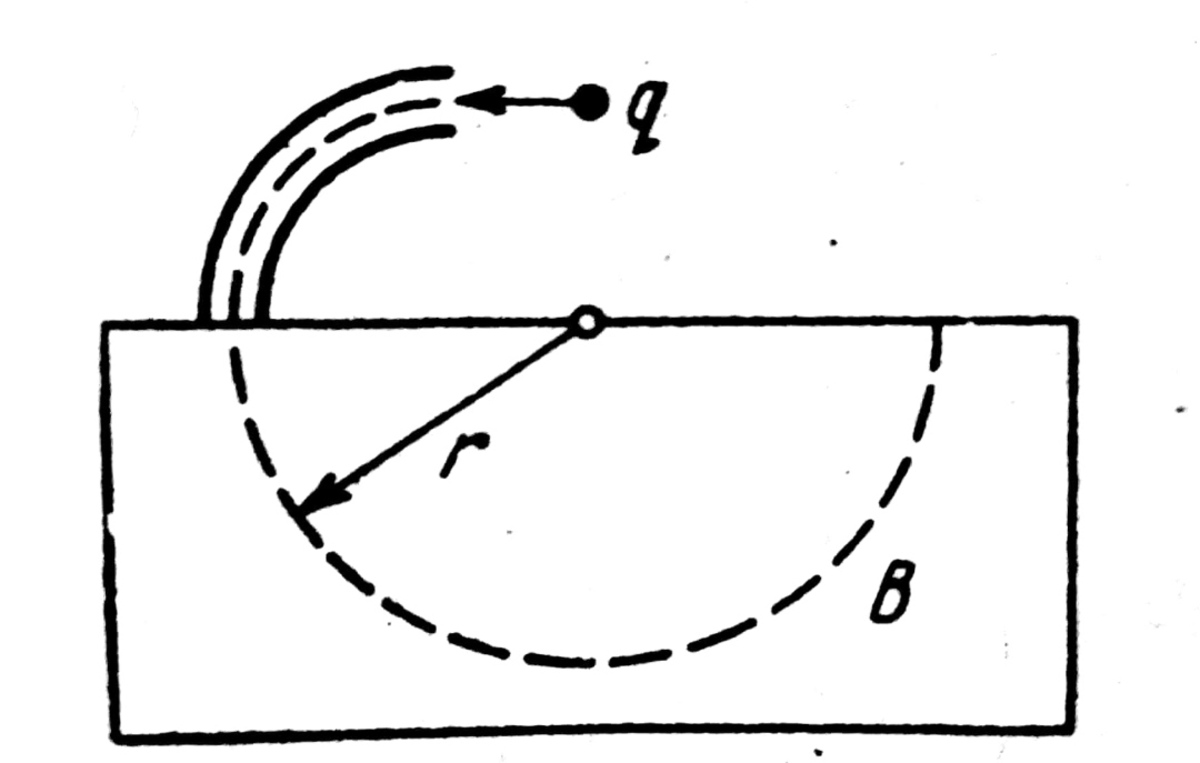 Find the specific charge
of the particle.
Find
Find the specific charge
of the particle.
Find
This problem is not original
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Motion through the capacitor :
r ln ( a b ) q V = r m u 2 ⟹ u 2 = m ln ( a b ) q V .
Motion through the magnetic field :
B q u = R m u 2 ⟹ u = m B q R .
So, m ln ( a b ) q V = m 2 B 2 q 2 R 2 ⟹ m q = B 2 R 2 ln ( a b ) V .
Hence the required sum is 1 + 1 + 1 + 2 + 2 + 1 + 1 = 9 .