Captain America's Shield

The areas of the circles (in descending order of area in square inches) are $225\pi$ , $132.25\pi$ , $81\pi$ and $36\pi$ respectively, hence the areas of the annuli (in descending order of area) are $92.75\pi$ , $51.25\pi$ and $45\pi$ respectively.

The areas of the smallest circle and the inscribed 5-pointed star however requires further work.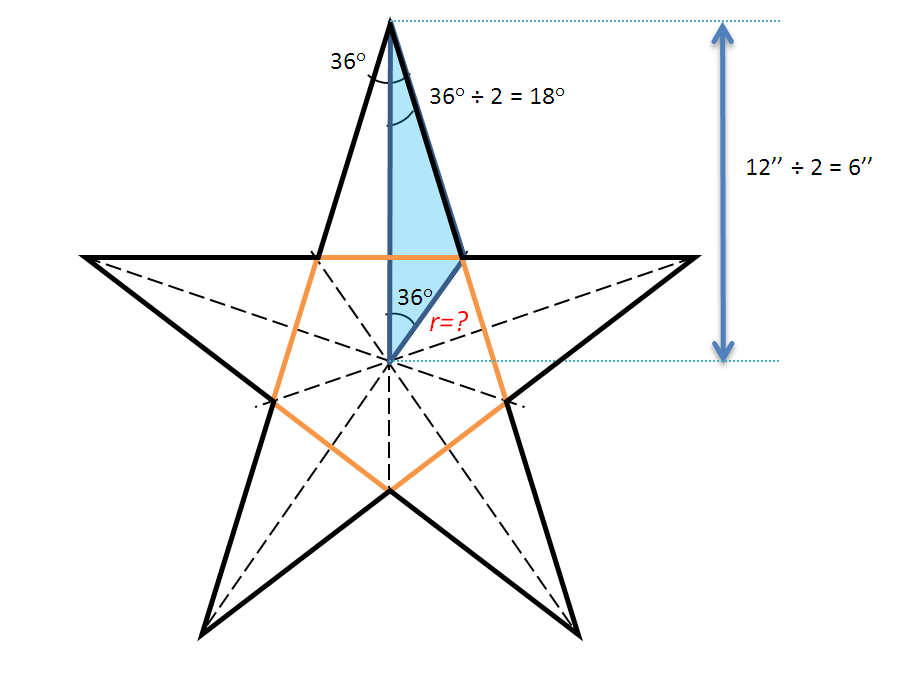 5-pointed stars are extended from a regular pentagon, and are most easily calculated as the area of 10 smaller triangles (in blue). The longest edge length of the blue triangle will then be half of the diameter of the smallest circle the star is inscribed in. The angles in the blue triangle can also be determined by properties of regular polygons :

• The angle subtended at the center of the pentagon by one of its sides = 72°, thus the angle at the bottom of the highlighted blue triangle is half of that i.e. 36°

• The angle at each point of a 5-sided regular star is 36°, hence the angle at the top of the highlighted blue triangle is half of that i.e. 18°

Then by using sine rule : $\frac{r}{\sin(18°)}=\frac{6}{\sin(180°-36°-18°)}$ which gives $r=2.292$ in.

Thus the area of one blue triangle, via sine rule , is: $\frac{1}{2} (2.292)(6) \sin(36°)=4.042$ and therefore the area of the star is 40.42 sq in., and hence the area of the blue region is $36\pi-40.42$ sq in.

Thus the required ratio of areas will be $\frac{92.75\pi+45\pi+36\pi-40.42}{51.25\pi+40.42}=2.5$ .