Carbon fusion
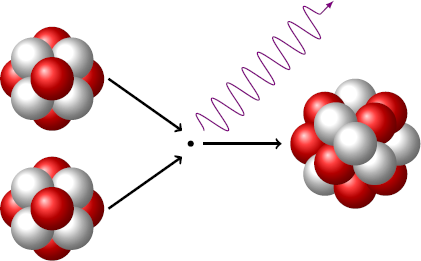
In massive stars, the fusion of carbon nuclei occurs according to the reaction 6 1 2 C + 6 1 2 C → 1 2 2 4 Mg + Δ E Estimate the energy Δ E released in this reaction (mostly in the form of gamma radiation). Use only classical continuum mechanics and electrostatics.
Assumptions and details :
-
The nucleons in the atomic core behave like an incompressible liquid with density ρ ≈ 2 ⋅ 1 0 1 7 kg / m 3 and surface tension σ ≈ 1 . 3 ⋅ 1 0 1 7 Nm .
-
The atomic nuclei have the shape of a sphere and are homogeneously electrically charged.
-
The following constants may be useful:
nucleon mass elementary charge vacuum permittivity m p ≈ m n e ε 0 ≈ 1 . 6 7 ⋅ 1 0 − 2 7 kg ≈ 1 . 6 ⋅ 1 0 − 1 9 C ≈ 8 . 8 5 ⋅ 1 0 − 1 2 Vm C
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we determine the nuclear radius R . The nuclei are spheres with a volume V = 3 4 π R 3 . The mass of a nucleus M ≈ m p A is porportional to the mass number A = Z + N . (The mass defect of the nucleons is neglected because it accounts for less than 1% of the mass.) Since the nuclei all have the same density, it results ⇒ ⇒ ρ = V M R R C R Mg = 3 4 π R 3 m p A = [ 4 π ρ 3 m p A ] 1 / 3 ≈ 2 . 8 8 ⋅ 1 0 − 1 5 m ≈ 3 . 6 3 ⋅ 1 0 − 1 5 m Only two contributions are important for the determination of the released energy: