Cardioid in coffee cup (part A)
You may notice there is light reflecting in the above coffee cup that looks like a cardioid (heart).
In fact, it is a cardioid, as illustrated below:
Here come a math question:
Let be the area bounded by the cardioid, and the area of the "whole" coffee surface (in the first picture).
Find the value of
Notation: denotes the floor function .
The answer is 666.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Support the blue curve is modeled as r = 2 ( 1 − sin θ ) , then the circle can be modeled as x 2 + ( y + 1 ) 2 = 3 2 .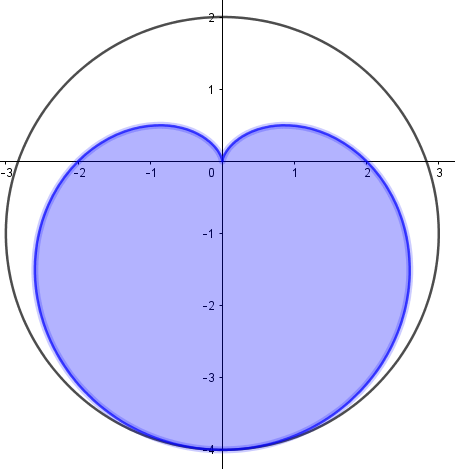
So B A = π × ( 3 ) 2 2 1 ∫ 0 2 π ( 2 ( 1 − sin θ ) ) 2 d θ = 9 π 6 π = 3 2 . So ⌊ B 1 0 0 0 A ⌋ = 6 6 6 .