Cards. Why Does It Have To Be Cards?

$\color{#EC7300}{\text{How many cards would Andrei not be able to all identify?}}$ My proposition is as follows:

Proposition: It is not possible to identify $1987=2013-26$ cards. This can be proven. We number the cards $A_1, A_2, \dots, A_{2012}, A_{2013}$ , and write the numbers $1 ,2, \dots, 2012, 2013$ on them respectively. We ask ourselves the question: can Kostya answer in such a way that Andrei would not be able to identify the numbers on cards $A_1, A_2, \dots, A_{27}$ ?

We can create a graph on the numbers $1$ to $N$ based on how Kostya relabels the cards, so a directed edge is drawn from $x$ to $y$ if card $x$ is relabeled with the number $y$ . It is clear this graph will be a bunch of disjoint cycles of length at least $2$ since every card is relabeled. Suppose that Kostya creates a graph for his permutation consisting of $9$ disjoint cycles of $3$ . For every $i=1,2, \dots, 9$ let us group the cards into triples $T_i$ like so: $A_{3i-2}, A_{3i-1}, A_{3i}$ will be cards in this triple. Now since Andrei selects $10$ cards, he will pick $2$ from the same triple by the Pigeonhole Principle $\color{#D61F06}{\text{(we have 9 triples and, since we pick 10 cards, this follows)}}$ , and these will be connected with a directed edge since cycles are length $3$ . So Andrei will pick $x$ and $y$ such that $x$ is relabeled with $y$ . Kostya will call out the card on the line between these two cards, and this works for the original set of $10$ cards since Andrei picked $y$ , and it works for the relabeled set since Andrei picked $x$ , so Andrei cannot get the card (as shown on the image).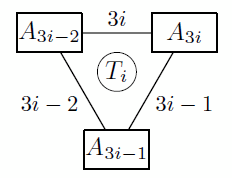

We notice that if on the cards $A_1, A_1, A_1$ stand the numbers $3,1,2$ (and not $1,2,3$ ) respectively, our answer will not change. Thus, there is no "uniqueness" in the triples, and we would not be able to identify any of the numbers on the cards. $_\square$

Now, we only need to prove that we would be able to identify all $k$ cards, where $k < 1987$ . This we will show by proving that by asking all possible questions about $28$ cards, then by the answers we will be able to identify the number on one of them and, subsequently, on all of them. For this we need the following lemma:

Lemma: Let's imagine that in a graph where vertices represent the cards there are at least $3n-2$ vertices and no more than $3n-2$ edges ( $n \geq 2$ ). We shall then be able to find $n$ vertices between which there are no edges.

Proof: Induction on $n$ . First of all, we notice that we can eliminate several vertices and add several edges to make both of these appear $3n-2$ )times.

Base When $n=2$ on $4$ vertices we must have less than $6$ edges, which means that one pair of points isn't connected. We can then choose this pair.

Induction: We shall name the number of edges leading to each of vertex $d_1, \dots, d_{3n-2}$ , then $d_1+\dots+d_{3n-2}=2(3n-2)$ . Therefore, we shall either find a number $d_i=<2$ and a number $d_j>2$ , or every vertex is connected by two edges. In the first instance, we eliminate from the graph the $i$ -vertex and the $j$ -vertex, as well as the sole neighbour of $i$ -vertex (if it exists); we eliminated no more than $3$ vertices and no less than $3$ edges. In the second instance let us eliminate any vertex (let its number be $i$ ) and its two neighbours; since their degree is $2$ , we eliminated no less than $3$ edges and exactly $3$ vertices. By induction, in the graph that still remains there will now be $n-1$ vertices with no edges between them-adding the $i$ vertex, we get the required collection of $n$ vertices (since we eliminated $i$ 's neighbours).

Back to the problem. Imagine that we asked all questions about $28$ cards, and let the numbers appearing in the answers be $c_1, c_2, \dots, c_n$ (for $k \leq 28$ ). For every $i=1,2, \dots, k$ we shall look at all the $10$ cards for which we got the number $c_i$ ; we shall call their intersection $S_i$ (this set is not empty, for it contains the card with the number $c_i$ ). If there is only one element in this set, then that is the card with the number $c_i$ on it, and we have identified it.

In the worst case scenario, in each of the sets of intersection there are at least $2$ elements. For every $i$ we shall choose two cards in $S_i$ and connect them with an edge. We shall have a graph in accordance with the lemma for $n=10$ , and in it, we can choose $10$ cards with no edges between them. The answer for these ten points will be some number $c_i$ . Therefore, in these ten points there will have to be a set $S_i$ , which implies that $2$ of the $10$ cards are connected by an edge. A contradiction, meaning that there is no worst case scenario!

So the answer is $\color{#69047E}{t=1986}$ .

---

Alternatively, suppose there are $28$ cards. Consider the graph which we discussed in the beginning. Notice that if Andrei can select $10$ cards that are not joined by an edge in the graph, he will be able to name every single one of them.. Note that for an odd cycle of length $2k+1$ Andrei can pick $k$ disjoint cards and an even cycle of length $2k$ Andrei can pick $k$ . Therefore, Andrei can pick $\frac {28-C}{2}$ cards where $C$ is the number of odd cycles in the graph. Since each odd cycle is of length at least $3$ , and we can have no cycles of length $1$ , we must have $C\le 8$ , so Andrei can pick $10$ cards not joined by an edge, which proves our claim.

Similar Problems : The following problems are either similar or use the same methods and principles.

Bribe The Friend

Bribe The Friend Again

100% Natural