Cases

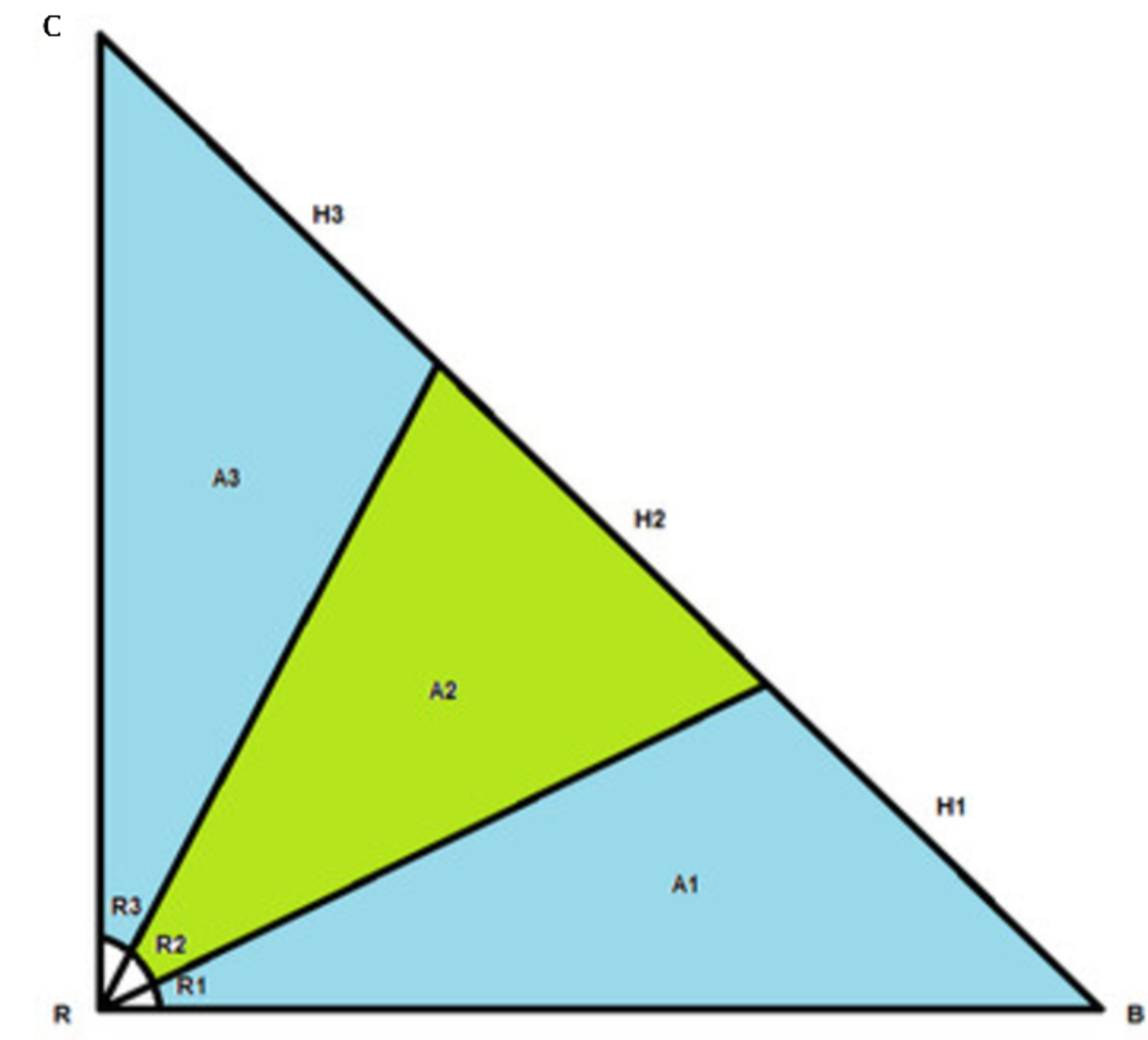
An isosceles right triangle RBC , R being the right angle , BC the hypotenuse . Two lines RM and RN divides the triangle into three triangles of areas A1,A2,A3 and the right angle to R1,R2,R3 and the hypotenuse to H1,H2,H3 respectively. Then we have three cases :

i) if R1 = R2 = R3 , then A1 : A2 ; A3 = 1 : (√a1 -1) : 1 and H1 : H2 : H3 = 1 : (√h1 -1) : 1

ii) if A1 = A2 = A 3 , then H1 : H2 ; H3 = 1 : h2 : 1 and SinR1 : SinR2 : SinR3 = 1 : r1/√5 : 1

iii) if H1 = H2 = H3 , then A1 : A2 ; A3 = 1 : a2 : 1 and tanR1 : tanR2 : tanR3 = 1 : r2/2 : 1

From the three cases above find the value of the expression : $\frac{a1r1h1}{a2r2h2}$