Trisected Area 2

For this problem, let's work with the bonus problem, which will help us answer the trisection problem.

---

Section I. $n$ -section Problem

---

The claim is:

For integer $n \geq 2$ , there are $2n - 3$ different ways to assign $\alpha$ and $\beta$ for the right triangle.

Consider the following diagram: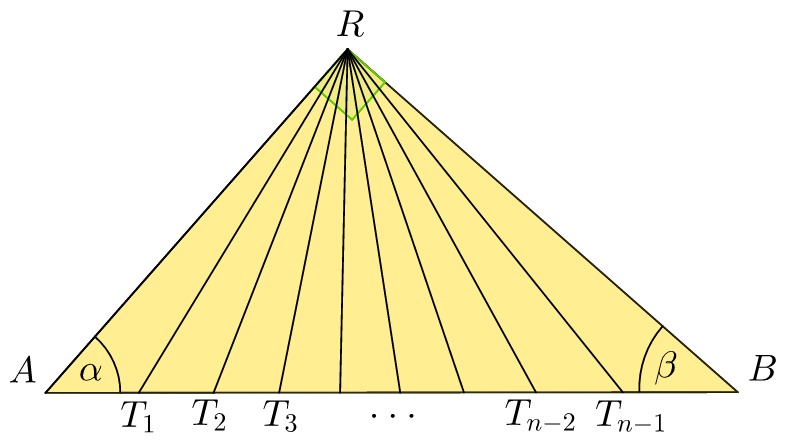 Figure 1. This is the $n$ -sected triangle with $n$ regions.

For each $n \geq 2$ , the right triangle is divided into $n$ regions, which implies this can be done with $(n - 1)$ cuts.

Because $n$ -secting the right angle gives $n$ angles of measure $\dfrac{90^{\circ}}{n}$ , each of the small triangles share these angles. For any pair of triangles to have the congruent areas, $\Delta BAR$ must be symmetrical with respect to the $n$ -section point since this forces (1) each pair of triangles to also be symmetrical and (2) them to share common side lengths and angle measures.

However, since there also exist some triangles other than $\Delta BAR$ that are the combinations of adjacent regions with the same angles, symmetry also takes place within each of these large triangles. In that case, we consider each of $\Delta T_jBR$ , where $1 \leq j \leq (n - 2)$ (see Note at the end of Case 2 why this suffices).

So we want to determine the possible angle choices of $\alpha$ and $\beta$ for $\Delta BAR$ and each of (\Delta T_jBR).

Subsection I.1. Case 1: $\Delta BAR$

If $\Delta BAR$ is the isosceles triangle, then $\alpha = \beta$ . But since $\Delta BAR$ is also the right triangle, this forces $\alpha = \beta = 45^{\circ}$ , which shows there is one way to assign $\alpha$ and $\beta$ .

Subsection I.2. Case 2: $\Delta T_jBR$

Let $k$ denote the arbitrary constant, such that $\alpha = k\beta$ . Determining the measurement of each $\angle RT_jB$ , we have $\angle RT_jB = \alpha + j \cdot \dfrac{90^{\circ}}{n} = k\beta + j \cdot \dfrac{90^{\circ}}{n}$ For $\Delta T_jBR$ to be isosceles, $\begin{array}{rl} k\beta + j \cdot \dfrac{90^{\circ}}{n} &= \beta\\ \beta\left(1 - k\right) &= j \cdot \dfrac{90^{\circ}}{n}\\ \beta &= \dfrac{90^{\circ}j}{n(1 - k)} \end{array}$ Since by the given $\begin{array}{rl} \alpha + \beta &= 90^{\circ}\\ k\beta + \beta &= 90^{\circ}\\ \beta\left(1 + k\right) &= 90^{\circ}\\ \beta &= \dfrac{90^{\circ}}{1 + k} \end{array}$ this implies $\begin{array}{rlccl} \dfrac{90^{\circ}}{1 + k} &= \dfrac{90^{\circ}j}{n(1 - k)}\\ \dfrac{1}{1 + k} &= \dfrac{j}{n(1 - k)}\\ n(1 - k) &= j(1 + k)\\ n - nk &= j + jk\\ n - j &= k(j + n)\\ k &= \dfrac{n - j}{n + j} \end{array}$ So $\begin{array}{rl} \beta &= \dfrac{90^{\circ}}{1 + k}\\ &= \dfrac{90^{\circ}}{1 + \frac{n - j}{n + j}}\\ &= \dfrac{90^{\circ}(n + j)}{n + j + n - j}\\ &= \dfrac{90^{\circ}(n + j)}{2n} \end{array}$ which shows that $\begin{array}{rl} \alpha &= k\beta\\ &= \dfrac{n - j}{n + j} \cdot \dfrac{90^{\circ}(n + j)}{2n}\\ &= \dfrac{90^{\circ}(n - j)}{2n} \end{array}$ Since $1 \leq j \leq (n - 2)$ , it is impossible for either $\alpha$ or $\beta$ to be $45^{\circ}$ . In that case, since there are two distinct values for $\alpha$ and $\beta$ , and we counted $(n - 2)$ subtriangles of $\Delta BAR$ , we found that there are $2(n - 2)$ more ways to assign $\alpha$ and $\beta$ .

Note: No matter how you find the values of $\alpha$ and $\beta$ from other large triangles, since the $n$ -sected angles of $\Delta BAR$ are symmetric, the results are still the same. For instance, if I choose $\Delta T_1T_{n-1}R$ , then $\begin{array}{rl} \alpha + \dfrac{90^{\circ}}{n} &= \beta + \dfrac{90^{\circ}}{n}\\ \alpha &= \beta \end{array}$ which is already found from Case 1 . Likewise, if I choose $\Delta T_1T_{n}R$ , then the results already appear from the previous computation.

Subsection I.3. Result

We have proven that there are $2(n - 2) + 1 = \boxed{2n - 3}$ unique choices for $\alpha$ and $\beta$ .

$\square\text{ Q.E.D.}$

---

Section II. Trisection Problem

---

Figure 2. Trisected right triangle.

Since the right angle is trisected, there are $3$ congruent angles of $30^{\circ}$ . From the general case, since $n = 3$ , the answer is $2(3) - 3 = \boxed{3}$ ways to choose $\alpha$ and $\beta$ .