Catch a Star
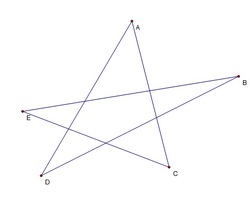 Find
∠
D
A
C
+
∠
E
B
D
+
∠
A
C
E
+
∠
B
D
A
+
∠
C
E
B
Find
∠
D
A
C
+
∠
E
B
D
+
∠
A
C
E
+
∠
B
D
A
+
∠
C
E
B
Give you answer in degrees.
The answer is 180.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let's mark intersection points between A and C as P and Q ( B E ∩ A C = P and B D ∩ A C = Q ). Then ∠ B P Q = ∠ C + ∠ E and ∠ B Q P = ∠ A + ∠ D
Therefore the sum of angles in a star equals to the sum of angles in a triangle:
∠ A + ∠ B + ∠ C + ∠ D + ∠ E = ∠ B + ∠ P + ∠ Q = 1 8 0
Sum of the the exterior angles of every polygon is 360. sum of the exterior angles of then interior pentagon is 360. If we extend each side of the pentagon in the same direction then the sum of all the exterior angles will be 360. And also if we extend the each side in opposite direction then again sum of eterior angles will be 360. Adding both sums 360+360=720 sum of all the outer triangles 5*180=900 THEN SUM OF THE GIVEN ANGLES WILL BE 900-720=180.