Catch the Thief!
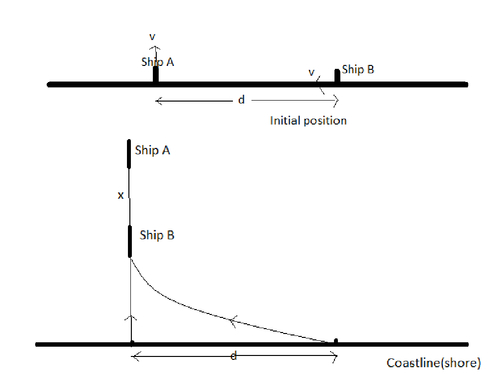
Two ships A and B are originally at a distance d from each other depart at the same time from a straight coastline. Ship A moves along a straight line perpendicular to the shore while ship B constantly heads for ship A , having at the each moment same as the latter. After a sufficiently great interval of time the second ship will be following the first one at a certain distance x . Find x in the image above.
Details and Assumptions
-
d = 2 6 m
-
In final position they are in same straight line perpendicular to coastline ( track of A )
-
Their speeds are the same.
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Yeah thanks for the solution But how did you post solution even after reporting it?
Log in to reply
ohh , don't you know , now brilliant has Improved reporting feature . We can report , and then return back to question without if we don't want to see others report ! So I reported and then revert back to question !
You should read this exciting features info click here
This question can be solved using polar coordinates.
d t d r = v sin θ − v
and v cos θ = r d t d θ
Now dividing both the equations we get:-
r d θ d r = cos θ sin θ − 1
Integrating this expression: ∫ d r r d r = ∫ 0 π / 2 c o s θ sin θ − 1 d θ
We get ln d r = − ln 2
hence answer is d/2
Sorry I'am replying late , Since I was little Busy in my JEE prep. , and Gautam , thanks for adding Diagram ,It is easy, It is actually Similar Problem Like as dog-cat chase , but in that problem finally dog will catch the cat means x=0 , but here It is not possible Since Velocities are same , But okay For Solution to this problem , Let at time t=t : distance b/w ship-A and Ship-B as ' r ' . Now Since their separation is changing
continuously . So we use relative velocity concept , Also Let Line Joining their separation and the Line of motion of ship -A (Vertical Line) has angle θ b/w them.Also Let final time is t=T.
d t − d r = v cos θ − v ∫ d x − d r = ∫ 0 T ( v cos θ − v ) d t . . . . ( 1 )
Now , Also difference b/w horizontal distance travelled by the two ships is equal to 'x' , So :
x ≡ ∫ 0 T v d t − ∫ 0 T v cos θ d t . . . . ( 2 )
using 1 and 2 we get ,
x = 2 d
Hopes this helps you!