Catenary?

Geometry Level 2

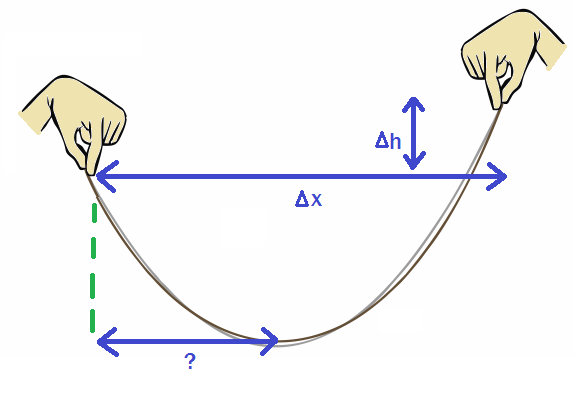
If you dangle a chain, as shown in the picture above, it forms a hyperbolic cosine function.

Assume the following values:

$\Delta h = 6$ inches
$\Delta x = 2$ feet.

What is the distance from the left (lower) side to the lowest point of the chain, in inches?

Give your answer to $2$ decimal places.

If you think the answer can't be determined, please put 99999.

Image credit: https://methmath.wordpress.com

The answer is 99999.

1 solution

Geoff Pilling
Jan 27, 2017

Depending on the length of the chain you will have different answers, as there are infinite hyperbolic cosine functions which have the same boundary conditions, as shown here:

Each will have a different value varying from $-\infty$ to $\frac{\Delta x}{2}$

So, the answer is $\boxed{99999}$

Image credit: https://en.wikipedia.org

I was trying to work out the locus of the vertices for different chain lengths but that was a mess. Anyway, it did seem intuitive that as the chain shortens, the vertex drifts to the left, (along an inverted parabolic path, perhaps?). If we were given the chain length then we could solve for the mystery distance but it would involve a non-algebraic system of 3 equations, 3 unknowns, which I would just as well leave to WolframAlpha.

Brian Charlesworth - 4 years, 4 months ago

Hmmmm... Interesting problem... The shape the locus of all the vertices traces out. I'm not sure its quite parabolic since I think it asymtotically approaches the line $x = \frac{\Delta x}{2}$ as the length $\rightarrow \infty$

Geoff Pilling - 4 years, 4 months ago

why not 11.98 inches

xiaosheng wei - 1 year ago

Catenary?

The answer is 99999.

1 solution

0 pending reports