Cat's Logic
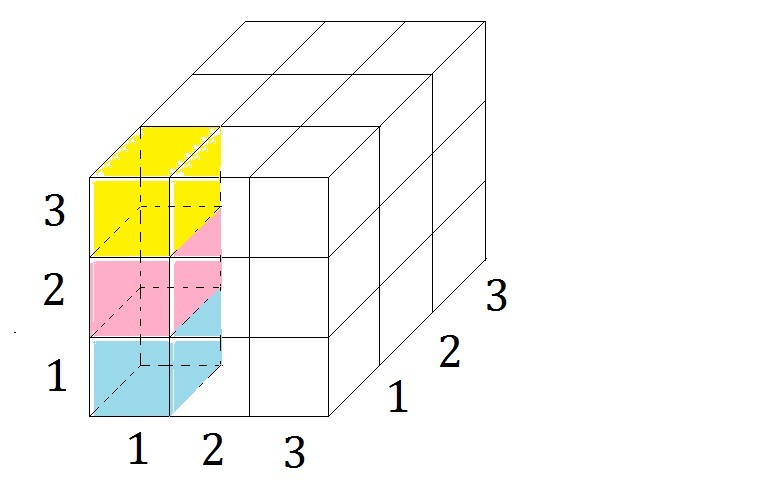
Albert the cat is living in one of the cubic cat condominium rooms, where every room has conjoined cat doors on all sides including the top and bottom (but no diagonal connection), and the cat can pass through any door in any direction if he so chooses.
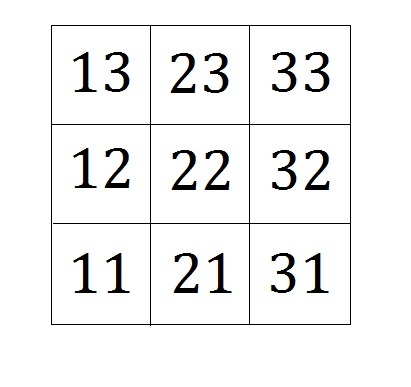
All condominium rooms are labeled with 3-digit numbers from 1-3. The first digit is the floor number while the other 2-digit combination can be laid out as shown in the table above. For example, in this 3D model, the room numbers are 111 for the blue, 211 for the pink, and 311 for the yellow, etc.
You know that Albert is living somewhere on the third floor, and after interviewing his neighbor cats, whose rooms he needs to pass in respective order, this is the information you've got:
Cat #1: I'm living in one of the corner rooms on the first floor. Albert always comes in my room first.
Cat #2: My room number is even.
Cat #3: The sum of my room number digits is .
Cat #4: The sum of the 3 digits can divide the room number itself.
Cat #5: My room number is prime with no repeated digits. Albert's room is just next door.
Assuming Albert never retraces his steps en route to his room, what is his room number?
The answer is 323.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1) First floor's corner rooms.
==> #1 = { 111, 113, 131, 133 }
2) Even room.
==> #2 = { 112, 132 }
3) Digit sum = 5. Then previously (#2) must have digit sum of either 4 or 6. If 4, there are 3 possible directions. If 6, only 2 possibilities.
==> #3 = { 113, 212, 122, 131 }
4) This is the second last instruction, so by now must already reached the second floor. Room number is divisible by digit sum, with the previous (#3) being equal to 5, can only be 4 or 6 (current digit sum = previous digit sum ± 1). If so, then the room number must also be even as to enable a division by an even number. #3 at 113 or 131 is incapable of fulfilling both conditions in one go (up the stairs AND evening the odds).
==> #4 = { 312, 222 }
5) This is the last instruction, so by now must already reached the third floor. Room number is prime with no repeated 1 digits. Forcing #4 at 222 upstairs will leave us with a composite room number (even), and between 311 and 313, it's obviously the latter.
==> #5 = { 313 }
6) Albert room's next door with no retracing involved. Between 312 and 323, we know it's the latter since 312 is occupied by #4.
Answer = 323