Cause you burn with the brightest flame

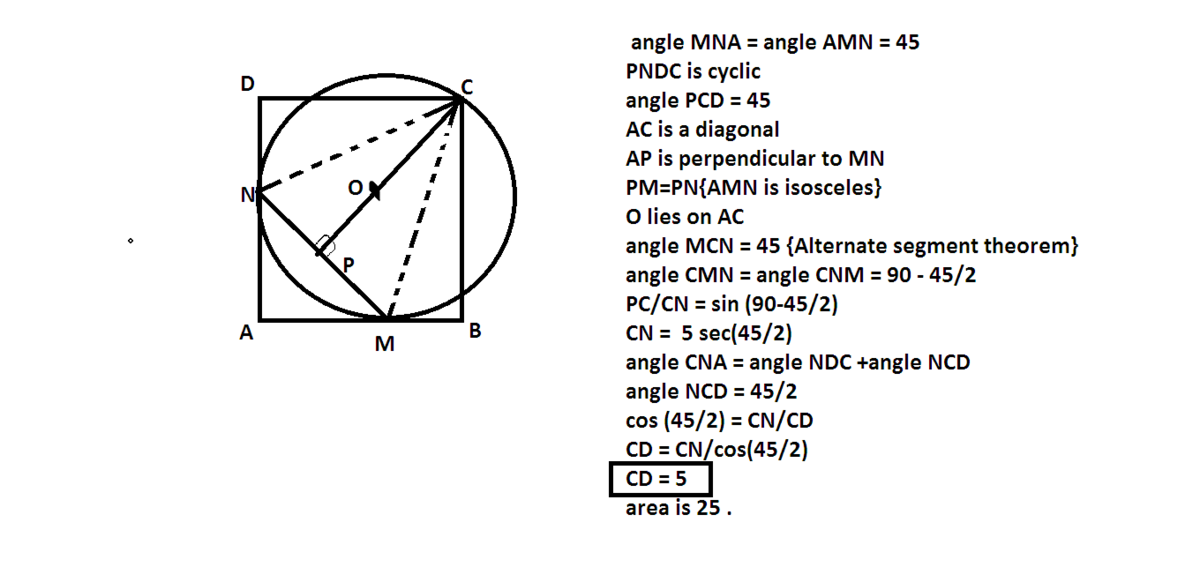
Very nice problem.

So, we have that $CT$ (picture) is $5$ . Because the circle only touches $AB$ and $AD$ , it is obligated that the circle's radius forms right angle with both segments. Therefore, we can represent $CT$ as $r + \frac{r \sqrt{2}}{2}$ . Thus, we can say that $r = \frac{10}{2 + \sqrt{2}}$ .

Now, let's focus on $a$ ( $\square ABCD$ 's side). $AM$ is obviosly $r$ ( $AMON$ is square) and $MB$ will be $\frac{r \sqrt{2}}{2}$ , therefore $a = r \times \frac{2 + \sqrt{2}}{2}$ .

When we use swap $r$ with $\frac{10}{2 + \sqrt{2}}$ , we get that $a = \frac{10}{2 + \sqrt{2}} \times \frac{2 + \sqrt{2}}{2}$ , and that is $a = 5$ .

From this point, further explaining is not necessary. Solution is $25$ .

Here 's my solution .