Ceiling on the floor

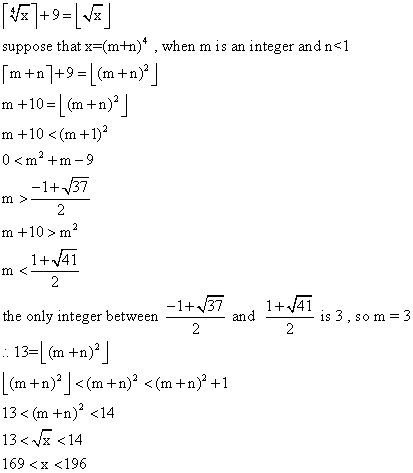
Let , $x=a^4+k$ where, $a^4\le a^4+k<(a+1)^4$ and, a and k are integer.

$a^4\le a^4+k<(a+1)^4\\a^4\le x<(a+1)^4\\a^2 \le \sqrt{x} < (a+1)^2\\a^2 \le \lfloor\sqrt{x}\rfloor < (a+1)^2$

Again,

$a^4\le a^4+k<(a+1)^4\\a^4\le x<(a+1)^4\\ a \le \sqrt[4]{x}<(a+1)$

So, $a=\sqrt[4]{x}$ or $a < \sqrt[4]{x}<(a+1)$

If, $a=\sqrt[4]{x}$ Then, $\lceil \sqrt[4]{x} \rceil+9=\lfloor\sqrt{x}\rfloor\\a+9=a^2$

solving the equation we get , $a=\frac{1\pm\sqrt{37}}{2}$ which is not an integer.

So, it should be , $a < \sqrt[4]{x}<(a+1)$ , therefore $\lceil \sqrt[4]{x} \rceil =(a+1)$

If, $a^2 \le \lfloor\sqrt{x}\rfloor$ we get ,

\begin{aligned}\lceil \sqrt[4]{x} \rceil+9&=\lfloor\sqrt{x}\rfloor\\a+1+9&\ge a^2\\\frac{1-\sqrt{41}}{2}&\le a\le \frac{1+\sqrt{41}}{2}\\-1&\le a\le 3\tag{1}\end{aligned}

If, $(a+1)^2 > \lfloor\sqrt{x}\rfloor$ we get ,

\begin{aligned}\lceil \sqrt[4]{x} \rceil+9&=\lfloor\sqrt{x}\rfloor\\a+1+9&< a^2+2a+1\\\frac{-1-\sqrt{37}}{2}&\ge a \hspace{1cm}or, \hspace{1cm}\frac{-1+\sqrt{37}}{2}<a\\-3&> a\hspace{1cm} or,\hspace{1cm} 3<a\tag{2}\end{aligned}

Solving (1) and (2) we get, $a=3$

Let , $\lfloor\sqrt{x}\rfloor=a^2+s$ , where s is an integer and , $0\le s\le 2a$

$\begin{aligned}\lceil \sqrt[4]{x} \rceil+9&=\lfloor\sqrt{x}\rfloor\\a+1+9&=a^2 +s\\3+1+9&=3^2 + s\\s&=4\end{aligned}$

Therefore,

$\begin{aligned} \lfloor\sqrt{x}\rfloor&=a^2+s\\&=3^2+4=13\\13^2&\le x < (13+1)^2\\169&\le x < 196\\169&\le x \le 195\end{aligned}$

So , there are $195-169+1=\boxed{27}$ positive integers that satisfy the equation .

$Let~~f(X)=9-\lfloor X^.5 \rfloor+\lceil X^.25 \rceil........\therefore~for~f(X)=0,.............X^.5>9,~~~\implies~X>81.\\ 81^.25=3,......So~X>(9+3)^2=144=12^2..\\ Let X=13^2=169.\\ \therefore~f(169)=9-\lfloor 169^.5 \rfloor+\lceil (169)^.25 \rceil =9-13+\lceil 3.7.. \rceil =9-13+4=0. \\ When~\lfloor X^.5 \rfloor=14, ~f(14)>0.~~~~~~~~~~~14^2=196.\\ So~for~~X~from~169~to~196-1=195, ~we~will~get~f(X)=0.\\ \therefore~Number~ of~solutions=195-169+1=\Huge \color{#D61F06}{27}.$