Centbycent

In the above figure we have,

$\begin{aligned} \text{ The area of the orange triangle }&=\dfrac{1}{10} \times \text{ The area of the decagon }\\\\ &=\dfrac{1}{2}\times a \times h\\ \text{Required area }&= a \times 2h\\ &=4\times(\dfrac{1}{2}\times a \times h)\\ &=4\times (\text{ area of the orange triangle })\\ &=\dfrac{4}{10} \times \text{ area of the decagon }\\\\ &=40\% \text{ of the area of the decagon } \end{aligned}$

The shaded area can be divided into 8 congruent triangles, as pictured below, where the blue shaded area represents 1/10 or 10% of the area of the decagon.

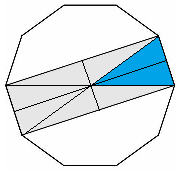
Since the blue shaded area is also 2 of the congruent triangles, each congruent triangle is 10% ÷ 2 = 5% of the area of the decagon. And since there are 8 congruent triangles shaded, the percentage of the shaded area is 8 · 5% = 40%.

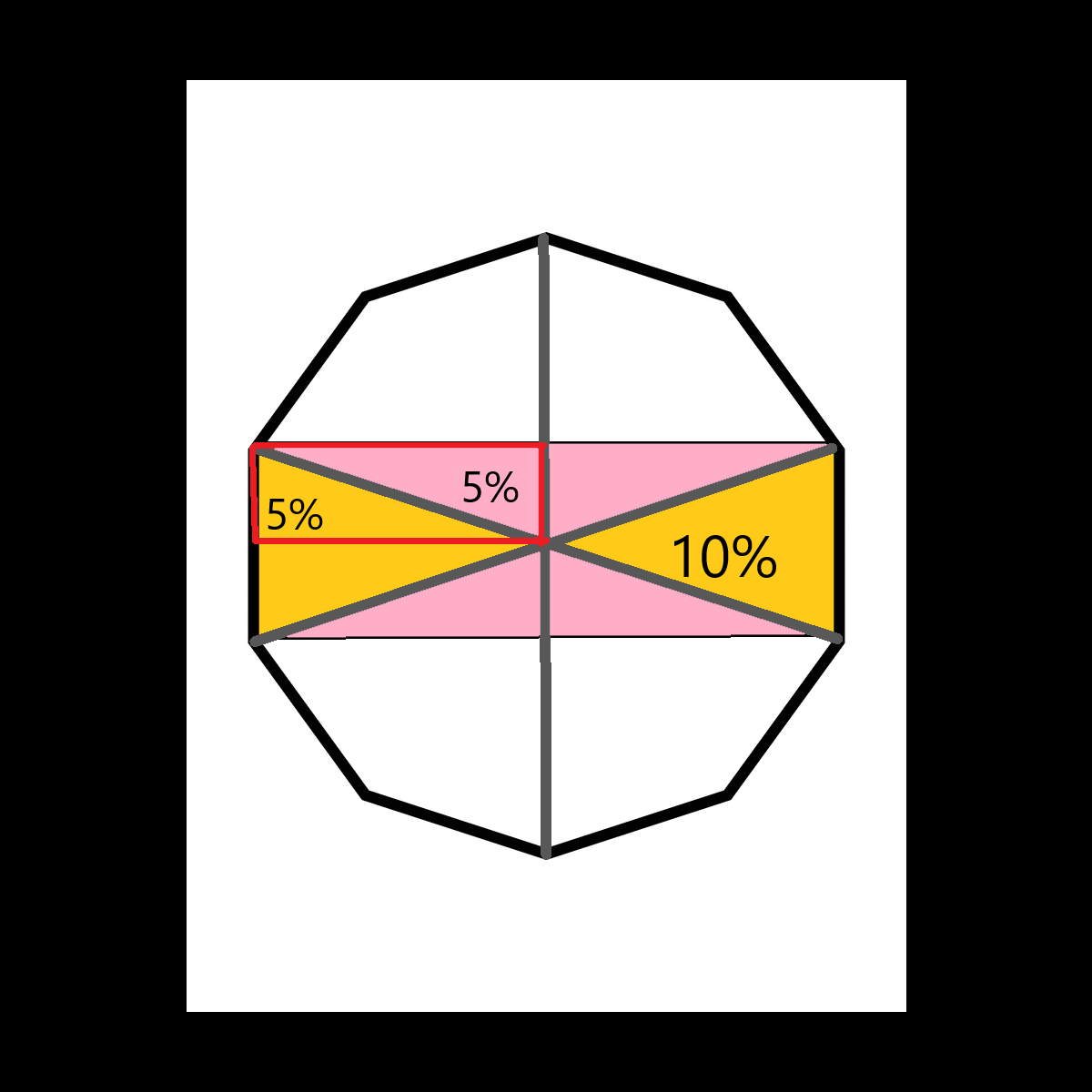Two triangles of the decagon are equal to 20% of its area. Of course, these triangles are equal. Half of the one of these triangles (=5%) create a parallelogram with the boundaries given. In that way the parallelogram is equally divided in two parts by the one side of the triangle. If half of the triangle is 5% (10% : 2 = 5%) then the other equal part of the parallelogram (the triangle in pink) must be 5% too. There are 4 equal pink triangles so 5% x 4 = 20% . Add the sum of the two orange triangles (20% as shown above) with the sum of the pink ones (20%) you have 40%.

let the side length of the decagon = a

The Shaded area A1 = $4{a}^2 cos36 cos18$

The total area of the decagon A2 = $\frac{10 {a}^2}{4tan18}$

then $\frac{A1}{A2}$ = 1.6 cos36sin18 = 1.6sin54sin18 = 0.40

percentage = 40 %

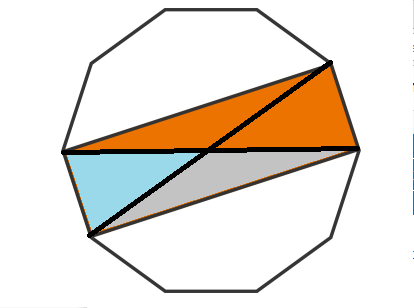Area of blue triangle is same as area of grey triangle as separated by median. grey triangle is 10% of total area and hence the rectangle is 40% area

All results given so far are of course correct, but I want to add simpler solution: The area of the rectangle ABFE is (2xCD)xAB. The area of the triangle ABC is (ABxCD)/2 and it is 1/10 of the area of the decagon. So the ratio of the area of the rectangle to that of the degagon is (2xCDxAB) / (10xABxCD)/2) = 2/5 = 40%

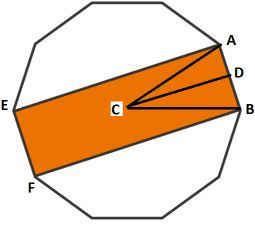
so with my extraordinary paint skills i drew this wich reflects my rather simple first thought quite acurately

Let’s say a is the apothem and p is the perimeter of the regular decagon, and the side length of the decagon is $\frac {p}{10}$ (the number of sides).

The area of the whole decagon can be found by the formula: $A = \frac {a \times p}{2}$

The area of the rectangle is: $A = b \times h = 2a \times \frac {p}{10} = \frac {a \times p}{5}$

Therefore, the ratio of the area of the rectangle to the area of the decagon is: $\frac {\frac {a \times p}{5}}{\frac {a \times p}{2}} = \frac {2}{5} =$ 40%

Quick estimate , if we approximate decagon as circle with area πR^2, then: length of 1 side is ~2π R/10 = 1/5 πR Area of rectangle is about 2R × 1/5 πR = 2/5 πR×R = = 2/5 πR^2 , so it is 2/5 of the decagon, which is 40%

Approximate method

Area of inscribing circle = pi() r.r

Approx Width or rectangle = 2 pi() r / 10

Approx Length of rectangle = 2 r

Approx Area of rectangle = 0.4 pi() r.r

= 40% of circle area

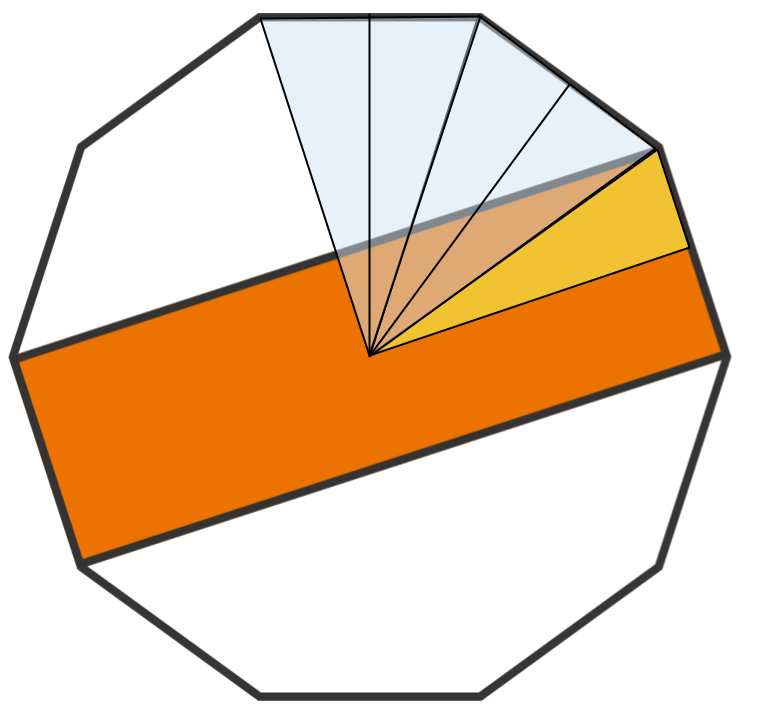
$\frac{1}{4}$ of the decagon consists of 5 congruent triangles.

$\frac{1}{4}$ of the shaded region consists of 2 of those triangles.

$\frac{2}{5}$ = 40%.

I saw it graphically first, but had to verify it with algebra. It’s very simple, though. Divide the area of the rectangle by area of decagon. (Sides are s, apothem is a)

Area rectangle: 2 X a X s

Area decagon: (.5 X a X s) X 10 = 5 X a X s (area of one triangle times 10)

(2 X a X s)/(5 X a X s)= (2/5)((aXs)/(aXs))=(2/3)= 40%

(David Vreken’s post has a picture showing the length of the rectangle is 2 X a.)

I figured the shaded of the decagon contained at least 10% of the decagon on both sides. This considered, I just needed to approximate the area on either side of that 10%. I thought that the area in the triangles either side of the 10% on both sides were exponentially decreasing infinitely which, in theory, suggests the area would eventually add to 20% on both sides. Therefore, I figured the area occupied by the orange shading equated to 40% that way. Criticism of my solution is very welcome.

I used the formula for the area of a regular decagon A = 2.5ad, where side length is a and d is the distance between parallel sides. Since ad is expressing the area in orange and 2.5x that is the whole area, 1/2.5 = 0.4, or 40% of the total area.

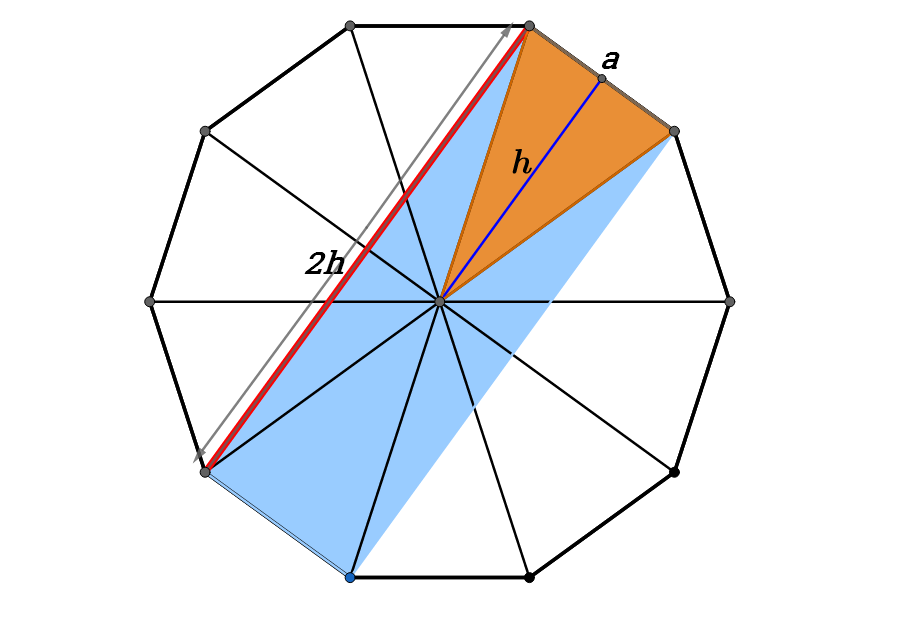
In general, from the diagram I borrowed above:

$A_{n- gon} = \dfrac{n}{2} ah$ and $A_{orangestrip} = 2ah \implies 2ah = \dfrac{x}{100} \dfrac{n}{2} ah \implies x = \dfrac{400}{n}$

Using $n = 10 \implies x =40\%$ .

Or using the actual areas:

Let $r$ be the radius of the circumscribed circle.

$a = 2r\sin(\dfrac{\pi}{n})$ and $h = r\cos(\dfrac{\pi}{n}) \implies A_{n-gon} = \dfrac{n}{2} \sin(\dfrac{2\pi}{n}) r^2$ and $A_{orangestrip} = 2\sin(\dfrac{2\pi}{n}) r^2 \implies$

$2\sin(\dfrac{2\pi}{n}) r^2 = \dfrac{x}{100} \dfrac{n}{2} \sin(\dfrac{2\pi}{n}) r^2 \implies x = \dfrac{400}{n}$

Using $n = 10 \implies x = 40\%$

Area of regular polygon = na²(cot π/n) ÷2 For decagon n=10, Area= 5a²cot 18° Area of rectangle = a × b.( b>a) % of area = b/ (a cot18°) × 20= 2× 20℅ =40%

Area of uncovered surface is symmetrical = 2×( area of 2 squares and area of 4 right angled triangle)

The area of the decagon is $5 s r$ where $s$ is the side length and $r$ is the apothem. If we now take a look at the rectangle, one of its sides has length $s$ and the other has length $2r$ so the area of the rectangle is $2sr$ . We can now compute $\frac{A_{rectangle}}{A_{decagon}} = \frac{2sr}{5sr} = \frac{2}{5}$ .