Center of Mass of a Circular lamina
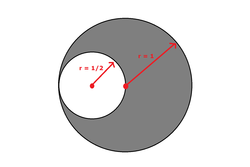 A solid disk of radius
1
and uniform density has a hole drilled through it, in the shape of a small circle of radius
2
1
. This small circle is tangent on the edge of the large circle.
A solid disk of radius
1
and uniform density has a hole drilled through it, in the shape of a small circle of radius
2
1
. This small circle is tangent on the edge of the large circle.
The distance from the geometric center of the large circle to the object's center of mass can be expressed as a 1 , where a is a positive integer. Find a .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I placed the origin of my x,y-coordinate system at the geometric center of the large circle. Since the object is symmetric about the x-axis, I considered only the top-half of the object. To make the integration simpler, I broke the object into two pieces: the quarter circle in quadrant I, and the quarter circle with a half-circle drilled out in quadrant II.
The center of mass (on x) for the first piece can be expressed as:
x ˉ 1 = π 4 ∫ 0 1 x 1 − x 2 d x
I evaluated this integral using the substitution:
u = 1 − x 2
d u = − 2 x d x , d x = − 2 x d u
u ( 0 ) = 1 , u ( 1 ) = 0
I flipped the negative sign and the limits of integration, so the integral becomes:
x ˉ 1 = π 2 ∫ 0 1 u 2 1 d u = 3 π 4
For the second region, I "cheated" and treated it as if it, too, were in quadrant I. Its center of mass integral is then:
∣ x ˉ 2 ∣ = π 8 ∫ 0 1 x 1 − x 2 − π 8 ∫ 0 1 x 4 1 − ( x − 2 1 ) 2 d x = A − B
The first integral "A" here is clearly twice the magnitude of x ˉ 1 . For the second integral "B," I used a trigonometric substitution:
x − 2 1 = 2 1 s i n θ
d x = 2 1 c o s θ d θ
θ ( 0 ) = − 2 π , θ ( 1 ) = 2 π
So this integral becomes:
B = π 1 ∫ − 2 π 2 π c o s 2 θ d θ + π 1 ∫ − 2 π 2 π s i n θ c o s 2 θ d θ = C + D
By inspection, the integral " D ," is 0 , so:
B = C = π 1 ∫ − 2 π 2 π 2 1 ( 1 + c o s 2 θ ) d θ = 2 1
So our center of mass for the second region is:
∣ x ˉ 2 ∣ = 3 π 8 − 2 1
Finally, the center of mass for the entire object is:
x ˉ = M m 1 x ˉ 1 − m 2 ∣ x ˉ 2 ∣ = 4 3 π 2 π ( 3 π 4 ) − 4 π ( 3 π 8 − 2 1 ) = 6 1
So:
a = 6
Can you please tell me how you got this sketch ? I use MS Accessary and Paint, down load to INGUR. I get small sketches or truncated ones!!
Assume a rectangular coordinate system with origin placed at the center of the original larger disc and the x -axis being the line passing through the origin and the center of the hole drilled. The y -axis is thus perpendicular to this line. Exploiting some symmetry, as equal masses are taken out from upper and lower portion of the x -axis, the y coordinate of the center of mass remains fixed at 0 . Thus the center of mass of the final object lies on the x -axis itself.
Let the surface mass density of the disc be σ . If we assume the hole is filled in again with the cut-out disc then the center of mass of the resultant body will be back at origin. Let m O and m H denote the masses of the final object and the hole respectively and the coordinates of their respective center of masses be x O and x H . Treating this as a two body system with center of mass at the origin and using the formula
x C M = m O + m H m O x O + m H x H
we get
⟹ ⟹ 0 = σ ( π ( r 2 − ( 2 r ) 2 ) ) + σ ( π ( 2 r ) 2 ) σ ( π ( r 2 − ( 2 r ) 2 ) ) ⋅ x O + σ ( π ( 2 r ) 2 ) ⋅ ( − 2 r ) 0 = 4 3 r 2 ⋅ x O − 8 r 3 x O = 6 r = 6 1
Thus, a = 6 .