Central Region Area
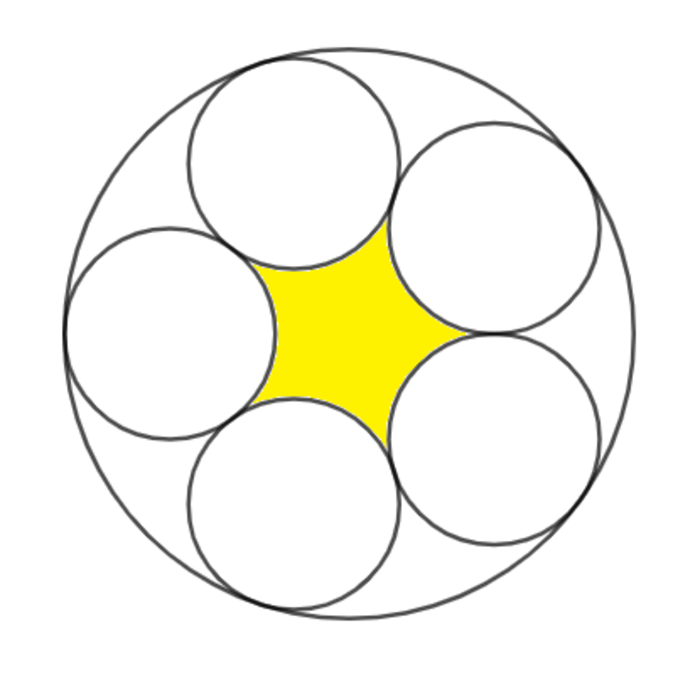
As shown above, five congruent circles are inscribed in a unit circle. The five circles surround a central region (shaded in yellow). Find the area A of this central region, and report ⌊ 1 0 4 A ⌋ .
The answer is 2973.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
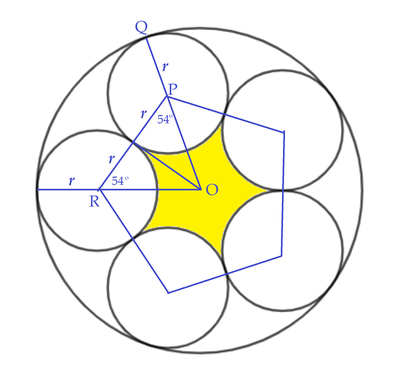
Let the radius of the five congruent circles be r . Join the centers of the five congruent circles with straight lines, we get a regular pentagon with side length of 2 r .
From the figure we note that O P + P Q = O Q ⟹ r sec 5 4 ∘ + r = 1 ⟹ r = 1 + sec 5 4 ∘ 1 .
Now consider one of the five congruent isosceles triangles that make up the pentagon. We note that one fifth of the yellow are is the area of △ O P R minus 3 6 0 ∘ 1 0 8 ∘ of the area of circle of radius r . Therefore the area of the yellow region:
A = 5 ( r 2 tan 5 4 ∘ − 3 6 0 1 0 8 π r 2 ) = ( 1 + sec 5 4 ∘ ) 2 5 ( tan 5 4 ∘ − 3 6 0 1 0 8 π ) ≈ 0 . 2 9 7 3 1 5 5 5 1 0 9 2
Therefore ⌊ 1 0 4 A ⌋ = 2 9 7 3 .
Solved it the same way, Chew-Seong......thanks for posting!
Label the points as follows:
Let the radius of the five congruent circles be r , so that R T = R S = r .
By symmetry, ∠ Q P T = 1 0 3 6 0 ° = 3 6 ° , and from right △ P R T we have ∠ P R T = 5 4 ° , P R = r sec 5 4 ° , and P T = tan 5 4 ° .
From P R + R S = P S we have r sec 5 4 ° + r = 1 , which solves to r = sec 5 4 ° + 1 1 .
The central yellow region is A = 1 0 A P Q T = 1 0 ( A △ P R T − A R Q T ) = 1 0 ( 2 1 r 2 tan 5 4 ° − 3 6 0 5 4 π r 2 ) = ( 5 tan 5 4 ° − 2 3 π ) r 2 .
Substituting r = sec 5 4 ° + 1 1 into A = ( 5 tan 5 4 ° − 2 3 π ) r 2 gives ⌊ 1 0 4 A ⌋ = 2 9 7 3 .