Central Region Perimeter
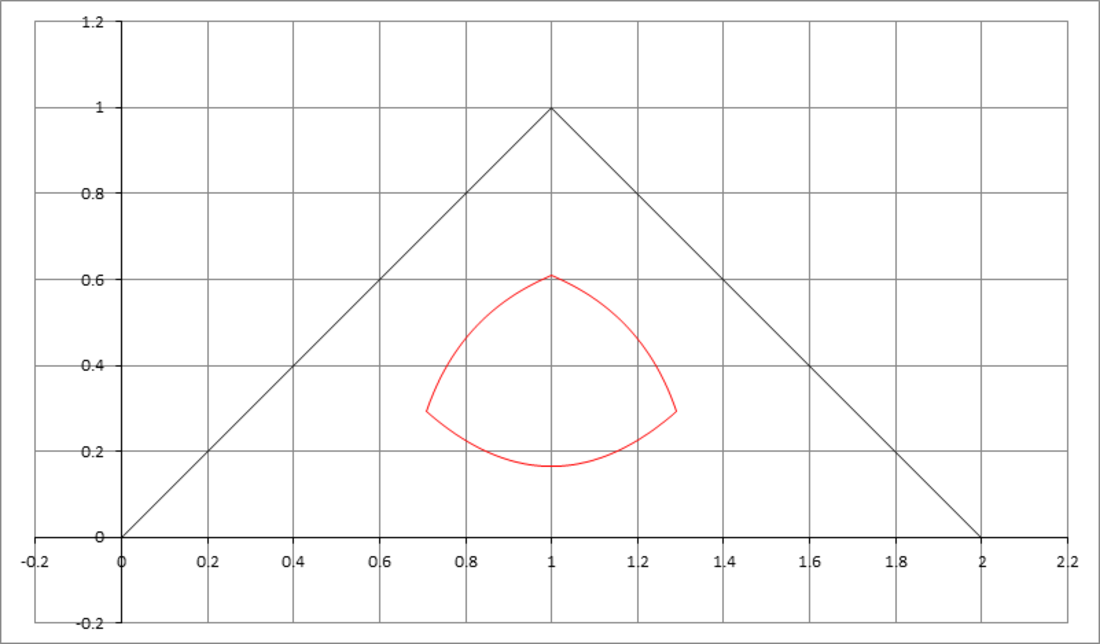
The figure above depicts a triangle with vertices . The red curve is the boundary of the region inside the triangle that is closer to the centroid of the triangle, than to any side. Find the length of this red curve.
The answer is 1.5367.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The locus of points which are equidistance from the centroid and an edge straight line is a parabola, where the centroid is the focus point F ( x f , y f ) and the edge straight line a x + b y + c = 0 is the directrix. And the equation of the parabola is given by ( reference ):
a 2 + b 2 ( a x + b y + c ) 2 = ( x − x f ) 2 + ( y − y f ) 2
To make the calculations easy, we set ( x f , y f ) = ( 0 , 0 ) or we move G ( x g , y g ) to G ′ ( 0 , 0 ) . Since x g = 3 x a + x b + x c = 3 0 + 2 + 1 = 1 and y g = 3 y a + y b + y c = 3 0 + 0 + 1 = 3 1 , then A ′ = ( x a − 1 , y a − 3 1 ) = ( − 1 , − 3 1 ) , B ′ = ( 1 , − 3 1 ) , and C ′ = ( 0 , 3 2 ) . Then the equation of the three parabolas are:
⎩ ⎪ ⎨ ⎪ ⎧ 6 y = 9 x 2 − 1 9 ( x − y ) 2 + 1 2 ( x + y ) − 4 = 0 9 ( x + y ) 2 − 1 2 ( x − y ) − 4 = 0 . . . ( 1 ) b o t t o m . . . ( 2 ) r i g h t . . . ( 3 ) l e f t
The region shaded blue, supposedly bounded by a red curve but I hate to redo the figure, is the part of the triangle which is nearer to the centroid G than an edge. Since the perimeter is symmetrical about the y-axis, we can find the length of curve of the right half and then multiply it by 2 .
From ( 1 ) , we get y = 2 3 x 2 − 6 1 = y 1 and from ( 2 ) , y = x + 3 2 2 − 6 x − 3 2 = y 2 . Let parabolas y 1 and y 2 meet at P ( a , b ) . From y 1 = y 2 , a = 3 1 − 2 + 2 2 − 1 . And the perimeter of the blue region:
p = 2 ∫ 0 a ⎝ ⎛ 1 + ( d x d y 1 ) 2 + 1 + ( d x d y 2 ) 2 ⎠ ⎞ d x = 2 ∫ 0 a ⎝ ⎛ 1 + ( 3 x ) 2 + 1 + ( 1 − 2 − 6 x 2 ) 2 ⎠ ⎞ d x ≈ 1 . 5 4