Centre of mass
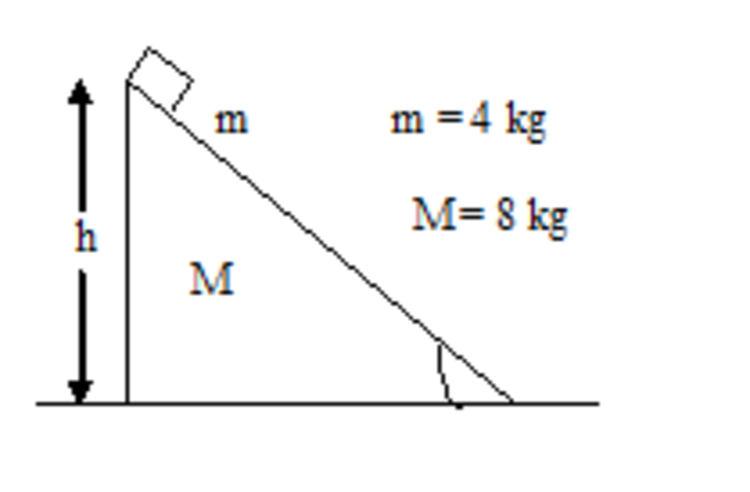 A wedge of mass
and a small block of mass
are kept on a horizontal surface as shown in the figure. All surfaces are smooth system is released from rest. Assume that system is placed at some planet of unknown gravity. If it given that at an instant it is given that the acceleration of wedge
is
. Then acceleration of centre of mass of block and wedge
will be? Take
.
A wedge of mass
and a small block of mass
are kept on a horizontal surface as shown in the figure. All surfaces are smooth system is released from rest. Assume that system is placed at some planet of unknown gravity. If it given that at an instant it is given that the acceleration of wedge
is
. Then acceleration of centre of mass of block and wedge
will be? Take
.
The answer is 1.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assume that the block of mass M moves with an acceleration A in negative x direction , and the block of mass m has a relative acceleration a r with respect to the block along the incline.
Now, since there is no external force, total force along horizontal direction can be equated to 0 : ⟹ M A + m ( A − a r cos θ ) = 0
and writing the net force equation on the block of mass m along the incline yields: m g sin θ = m ( a r − A cos θ )
Which on solving gives A = M + m sin 2 θ m g sin θ cos θ a r = M + m sin 2 θ ( M + m ) g sin 2 θ
Now , acceleration vectors of both the masses can be given by A = − M + m sin 2 θ m g sin θ cos θ i ^ a = ( a r cos θ − A ) i ^ − a r sin θ j ^ .
Note that acceleration of centre of mass will be given by A C O M = M + m m a + M A , and it can be noted upon by putting the values that acceleration of centre of mass remains in the vertical direction which was indeed true as there are no forces acting in the horizontal direction and thus centre of mass follows a straight line path downwards.
By substitutions, we get A C O M = − M + m sin 2 θ m g sin 2 θ j ^ .
Now, we can calculate the value of g by using the value of acceleration of M , which comes out to be 5 m s − 2 downwards.
Now, plugging in all the values, we obtain a c o m = 1 m s − 2 .