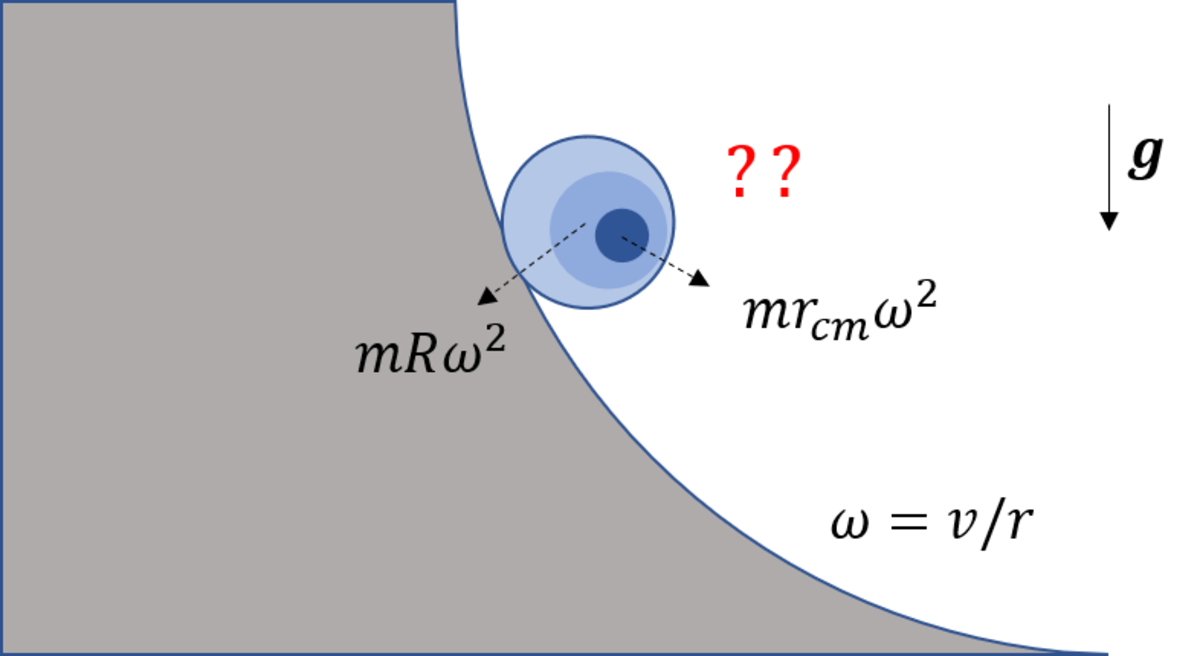
Centrifugal force on off-centered cylinders rolling down a curve
Let's say we have a cylinder of radius r with non-uniform density, resulting in a center of mass shifted away from center of geometry. Let's assume that this center of mass mid-way between center and circumference. So, r_cm = r/2.
Now, let's say this cylinder is rolling down on a curved path of radius R + r. Assume no slip condition.
What is the centripetal force on this cylinder? Does it have "two centripetal forces", from which we find a resultant?
I posed this question for discussion, not as a problem. (Answer is just 1.)
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Spin motion of the cylinder results in a centripetal acceleration since the C.M. is different from the geometric center. The orbital motion also gives rise to a centripetal acceleration. These two vectors do not have the same direction in general. The resultant centripetal acceleration is a vector sum of these two.