Centroid
The centroid of
is
.
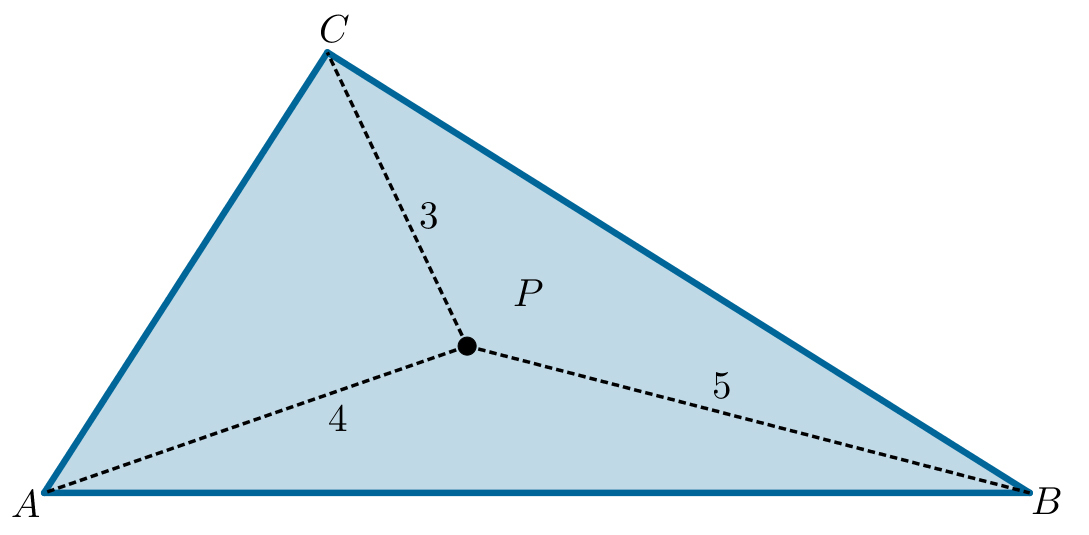
What is the area of the triangle, if and ?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The three medians divide the triangle into six smaller triangles, with the same area. The yellow triangle's sides are the one-thrid of each median. If the area of the A B C triangle is a, then the area of the yellow triangle is 2 1 ∗ 6 1 a = 1 2 1 a .
So there always exist a triangle, the sides of which are the one-third of each median of a triangle. The area of this, smaller triangle is one-twelfth of the larger triangle's area.
If a triangle's sides are 3 , 4 and 5 , then it is a right-angled triangle, and its area is 2 3 ∗ 4 = 6 . If we zoom out this triangle to its one-third, then we get the sought triangle, and its area is 1 . 5 . Therefore the big triangle's area is 1 2 ∗ 1 . 5 = 1 8 .